A la recherche du Nombre d’Or avec Tidyverse

Reading time ~ 5 minutes ->
Voici ce que Wikipedia nous donne comme définition :
Le Nombre d’Or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l’unique rapport a/b entre deux longueurs a et b tels que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égale à celui de la plus grande (a) sur la plus petite (b) c’est-à-dire lorsque :
\(\Large \frac{a+b} a = \frac ab\)
Le découpage d’un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ». Le nombre d’or est maintenant souvent désigné par la lettre \(\varphi\) (phi).
Ce nombre irrationnel est l’unique solution positive de l’équation
\(\Large x^2 = x + 1\).
Il vaut:
\(\Large \varphi ={\frac {1+{\sqrt 5}}2}\)
Sa valeur approximative est donc :
## [1] 1.61803398875Et sur un graphique ?
Enregistrons la formule dans un vecteur avec la fonction as_mapper du package Purrr.
gr.formula <- as_mapper(~ (.x^2 - .x - 1))Imprimons le graphique :
ggplot(data.frame(x = c(-2, 2)), aes(x)) +
stat_function(fun = gr.formula) +
theme_solarized_2() +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
geom_vline(xintercept = (1 + sqrt(5)) /2, col = "red", linetype = 5, size = 0.5) +
geom_hline(yintercept = 0, col = "red", linetype = 5, size = 0.5) +
annotate("point", x = (1 + sqrt(5)) /2, y = 0, size = 3, col = "red") +
labs(title = paste("Graphique de f(x) = (1 + sqrt(5)/2)"),
subtitle = "Phi ou Nombre d'Or equivaut à y = 0 pour x > 0",
x = "x",
y = "f(x)",
caption = " © DARP - 2018")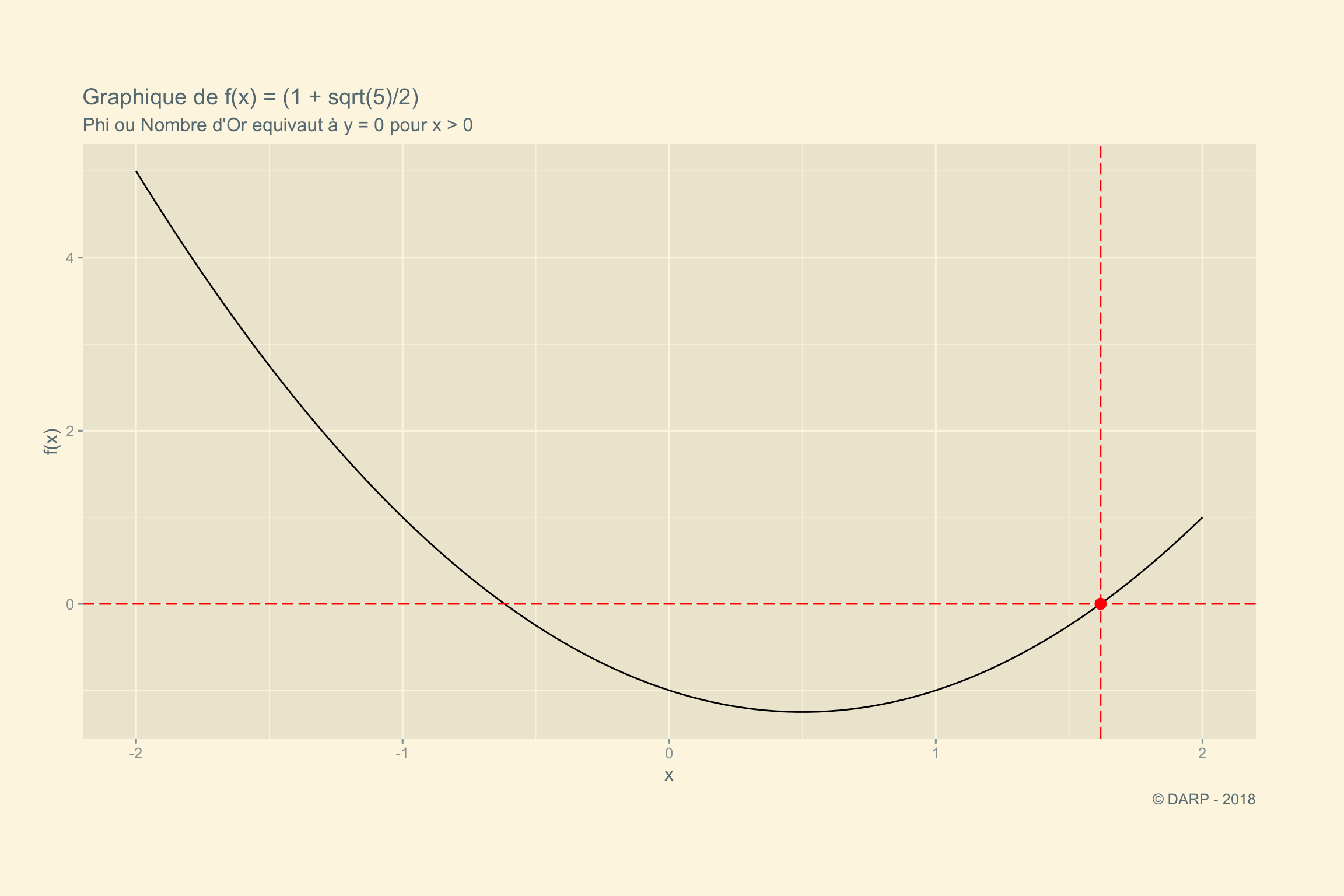
Nous pouvons avoir une intuition de la valeur de \(\varphi\) par la représentation graphique de l’équation. Nous voyons effectivement que pour
\(\Large y=0\).
2 valeurs de \(x\) sont possibles.
Le Nombre d’Or par fraction continue.
Nous pouvons atteindre le nombre réel par une fraction continue. Dans ce cas-ci elle est relativement simple :
\(\Large 1 + \frac{1} {1 + \frac1{1}}\)
Son prolongement à l’infini nous donne exactement le nombre d’or :
\(\Large 1 + \frac{1} {1 + \frac1{1 + \frac1{1 + \cdots}}}\)
Nous allons écrire une boucle qui va itérer la fraction jusqu’à atteindre une valeur assez approximative des premières décimales. Nous nommerons cette fonction golden_ratio(). Pour allez plus loin, nous allons positionner sur un graphique le résultat de chaque iétaration. Voici les étapes :
- Nous définissons une valeur par défaut pour les décimales, ici 10.
- Selon la valeur indiquée pour les décimales, nous l’appliquons à
options(digits = n) - Définition de variables d’initialisation :
- a = nombre de départ à fractionner,
- b = matrix de 100 rows,
- seq = le nombre d’itérations max souhaité pour la boucle
- La boucle
for(i in seq)c’est à dire autant de fois qu’il y a de rangées dansseq. Soit 100 itérations. - La condition
if()nous permet de mettre fin aux itérations dès que la valeur obtenue arrondie correspond à la valeur de \(\varphi\) arrondie à la décimale définie.
- Un graphique est dessiné avec les valeurs de chaque itération.
breakmet fin à la boucle. - Si le résultat de la condition
if()n’est pas vraie, une nouvelle itération est entamée avec un maximum défini dans la variableseq.
# Function code :
golden_ratio <- function(x, n.digits = NULL) {
# Step 1.
if(is.null(n.digits)) {
n <- 10
print("max digits by default (22)")
} else {
n <- n.digits
}
# Step 2.
options(digits = n)
# Step 3.
a <- x
b <- matrix(seq(1, 100, 1), ncol = 1)
seq <- seq(1, 100, 1)
gold.num <- (1 + sqrt(5)) /2
# Step 4.
for(i in seq) {
b[i] <- a
a <- 1/a
a <- a + 1
b[i + 1] <- a
# Step 5.
if(round(a, n) == round(gold.num, n)) {
a.round <- round(a, n)
lab <- paste("Le Nombre d'Or avec", n, "décimales trouvé après", i, "iterations :", a.round)
print(paste(n, "digits Golden Ratio found after", i, "iterations :", a.round))
b <- b[1:i]
b <- as.tibble(b)
b <- rowid_to_column(b)
# Step 6.
p <- ggplot(b, aes(rowid, value)) +
geom_line(col = "green4") +
geom_point() +
scale_x_log10(limits = c(1, nrow(b) + 10), labels = scales::number_format(accuracy = 0.01, trim = TRUE)) +
scale_y_continuous(labels = scales::number_format(accuracy = 0.01, trim = TRUE)) +
geom_hline(yintercept = gold.num, size = .6, col = "red", linetype = 3) +
theme_solarized_2() + theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
geom_vline(xintercept = nrow(b), col = "blue", linetype = 5, size = 0.5) +
annotate("label", x = nrow(b), y = last(b$value) + 0.3, angle = 90, label = a.round, fill = "blue", col = "white") +
annotate("label", x = 1.3, y = gold.num, , label = gold.num, fill = "red", col = "white") +
labs(title = paste("Calcul du Nombre d'Or avec", n, "décimales"),
subtitle = lab,
x = "Itérations",
y = "Valeur trouvée",
caption = " © DARP - 2018")
print(p)
gr <<- list(num = b,plot = p)
break
# Step 7.
} else {
print(paste("iteration #", i))
}
}
}Testons la fonction avec comme valeur de départ 1 et 12 décimales :
golden_ratio(1, n.digits = 12)## [1] "iteration # 1"
## [1] "iteration # 2"
## [1] "iteration # 3"
## [1] "iteration # 4"
## [1] "iteration # 5"
## [1] "iteration # 6"
## [1] "iteration # 7"
## [1] "iteration # 8"
## [1] "iteration # 9"
## [1] "iteration # 10"
## [1] "iteration # 11"
## [1] "iteration # 12"
## [1] "iteration # 13"
## [1] "iteration # 14"
## [1] "iteration # 15"
## [1] "iteration # 16"
## [1] "iteration # 17"
## [1] "iteration # 18"
## [1] "iteration # 19"
## [1] "iteration # 20"
## [1] "iteration # 21"
## [1] "iteration # 22"
## [1] "iteration # 23"
## [1] "iteration # 24"
## [1] "iteration # 25"
## [1] "iteration # 26"
## [1] "iteration # 27"
## [1] "iteration # 28"
## [1] "iteration # 29"
## [1] "12 digits Golden Ratio found after 30 iterations : 1.61803398875"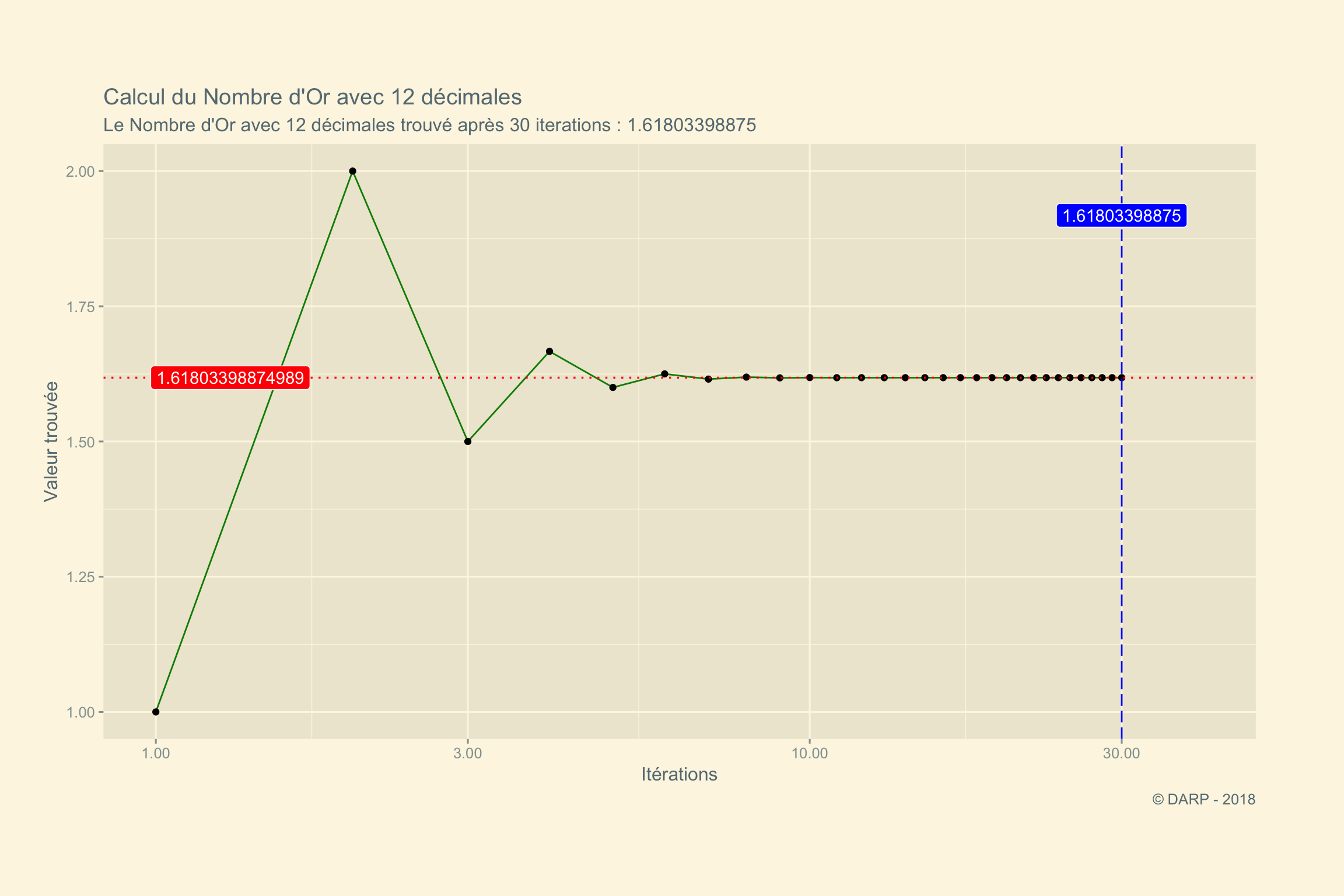
Il aura fallu 30 itérations, pour atteindre la valeur recherchée.
Résolution via uniroot
Une autre façon de résoudre l’équation \(x^2 - x - 1 = 0\) est l’utilisation de la fonction uniroot(). Nous définissons un vecteur pour indiquer l’amplitude de recherche de la valeur. La valeur trouvée est 1.61802823421 après 6 itérations. Nous n’obtenons pas les mêmes valeurs pour les décimales. Ne nous attardons pas trop sur cette fonction et cherchons d’autres méthodes pour résoudre l’équation.
uniroot(gr.formula, c(0,2))## $root
## [1] 1.61802823421
##
## $f.root
## [1] -1.28675203486e-05
##
## $iter
## [1] 6
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.10351562507e-05Résolution par “Brute Force” d’une séquence de nombres.
Nous allons essayer de trouver la valeur de \(x\) par “Brute force”, c’est à dire en testant toutes le valeurs avec le nombre de décimales souhaitées ! Ouch… ça va faire beaucoup :-). En effet pour n décimales d’un même nombre, nous avons \(10^n + 1\) valeurs possibles.
length(seq(0, 1, 0.0001))## [1] 10001Chaque valeur sera attribuée à \(x\) et le résultat enregistré. La valeur se rapprochant le plus de 0 sera conservée. Nous allons utiliser la fonction map() du package purrr pour le style. Nous verrons une autre façon de faire plus loin.
La séquence est la suivamte :
- Nous définissons l’équation avec
as_mapper. - Nous enregitrons le nombre de décimale dans le vecteur
d. La formule transforme la valeur induquée dans la fonction en décimale. - Une suite de nombre est formée avec comme intervalle le nombre de décimales.
- La fonction
mapapplique la formule définie avecas_mapper. - Nous enregistrons pour chaque résultat la valeur de \(x\) comme nom avec
set_names. - Nous transformons la liste en vecteur.
- Nous recherchons l’index de la valeur se rapprochant le plus de
0. - Nous enregistrons le nom de cette valeur qui n’est autre que notre valeur de \(x\) et notre Nombre d’Or (\(\varphi\))!
# Function code :
brute_seq_golden_ratio <- function(d) {
# Step 1.
gr.formula <- as_mapper(~ (.x^2 - .x - 1))
# Step 2.
n.decimal <- d/(d*(10^d))
# Step 3.
inter.val <- seq(0, 10, n.decimal)
# Step 4.
result.1 <- map(inter.val, gr.formula)
# Step 5.
result.1 <- result.1 %>% set_names(inter.val)
# Setp 6.
result.2 <- unlist(result.1)
# Step 7.
num.index <- which.min(abs(result.2))
# Step 8.
found <- names(result.2[num.index])
# Setp 9.
return(found)
}Testons notre fonction avec 3 décimales. Cela va relativement vite.
brute_seq_golden_ratio(3) #Ici avec 3 décimales## [1] "1.618"Le nombre à été trouvé après 24 millisecondes soit 0.024seconde.
microbenchmark::microbenchmark(brute_seq_golden_ratio(3), times = 5) #Ici avec 3 décimales## Unit: milliseconds
## expr min lq mean median
## brute_seq_golden_ratio(3) 20.627262 21.283796 23.626623 21.887198
## uq max neval
## 26.831685 27.503174 5Testons notre fonction avec 5 décimales ! soit 100.001 nombres à tester !
## [1] "1.61803"Le temps pour trouver la valeur est de `0.21 seconde. Plus ou moins 10xplus. Nous pourions en déduire :
- 3 décimales, 1.001 valeurs : 0.024 seconde -> 1.618
- 4 décimales, 10.001 valeurs : 0.21 seconde -> 1.6180
- 5 décimales, 100.001 valeurs : 2.5 secondes -> 1.61803
- 6 décimales, 1.000.001 valeurs : 45 secondes -> 1.618034
- 7 décimales, 10.000.001 valeurs : pffff beaucoup trop long…
microbenchmark::microbenchmark(brute_seq_golden_ratio(1), times = 5)## Unit: microseconds
## expr min lq mean median uq
## brute_seq_golden_ratio(1) 459.809 460.719 547.8944 556.312 590.225
## max neval
## 672.407 5microbenchmark::microbenchmark(brute_seq_golden_ratio(2), times = 5)## Unit: milliseconds
## expr min lq mean median uq
## brute_seq_golden_ratio(2) 2.261945 2.269496 2.3822494 2.28004 2.483955
## max neval
## 2.615811 5microbenchmark::microbenchmark(brute_seq_golden_ratio(3), times = 5)## Unit: milliseconds
## expr min lq mean median
## brute_seq_golden_ratio(3) 22.768749 24.101118 26.9095106 26.694767
## uq max neval
## 29.426074 31.556845 5microbenchmark::microbenchmark(brute_seq_golden_ratio(4), times = 5)## Unit: milliseconds
## expr min lq mean median
## brute_seq_golden_ratio(4) 250.034723 281.643192 295.8157818 295.402943
## uq max neval
## 304.939758 347.058293 5microbenchmark::microbenchmark(brute_seq_golden_ratio(5), times = 5)## Unit: seconds
## expr min lq mean
## brute_seq_golden_ratio(5) 3.041000426 3.158101974 3.4490801448
## median uq max neval
## 3.174545194 3.319114583 4.552638547 5microbenchmark::microbenchmark(brute_seq_golden_ratio(6), times = 1)## Unit: seconds
## expr min lq mean
## brute_seq_golden_ratio(6) 50.602960075 50.602960075 50.602960075
## median uq max neval
## 50.602960075 50.602960075 50.602960075 1Il semble que le temps de recherche soit exponentiel. Voyons cela sur un graphique. Malheureusement stat_smooth ne peut pas faire de prédiction avec la méthode “loess”, nous devons donc nous contenter d’une régression linéaire qui montre difficilement la prévision du temps en fonction du nombre de décimales recherchées. Appliquons une fonction \(x^3\) comme référence.
time_to_run <- tibble(decimal = c(1:6), time = c(0.000458, 0.0021, 0.023, 0.27, 2.30, 44.80))
time_to_run %>%
ggplot() +
aes(decimal, time) +
geom_line() +
geom_point() +
stat_smooth(method = "lm", fullrange = TRUE) +
stat_function(fun = as_mapper(~ (.x^3)), col = "red", linetype = 3) +
scale_x_continuous(breaks = c(1:10), limits = c(0, 10)) +
scale_y_continuous(limits = c(0, 200)) +
ggthemes::theme_solarized_2() +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
labs(title = paste("Temps d'exécution de la fonction selon le nombre de décimales"),
subtitle = "brute_seq_golden_ratio",
x = "Nombre de décimales",
y = "temps (en secondes)",
caption = " © DARP - 2018")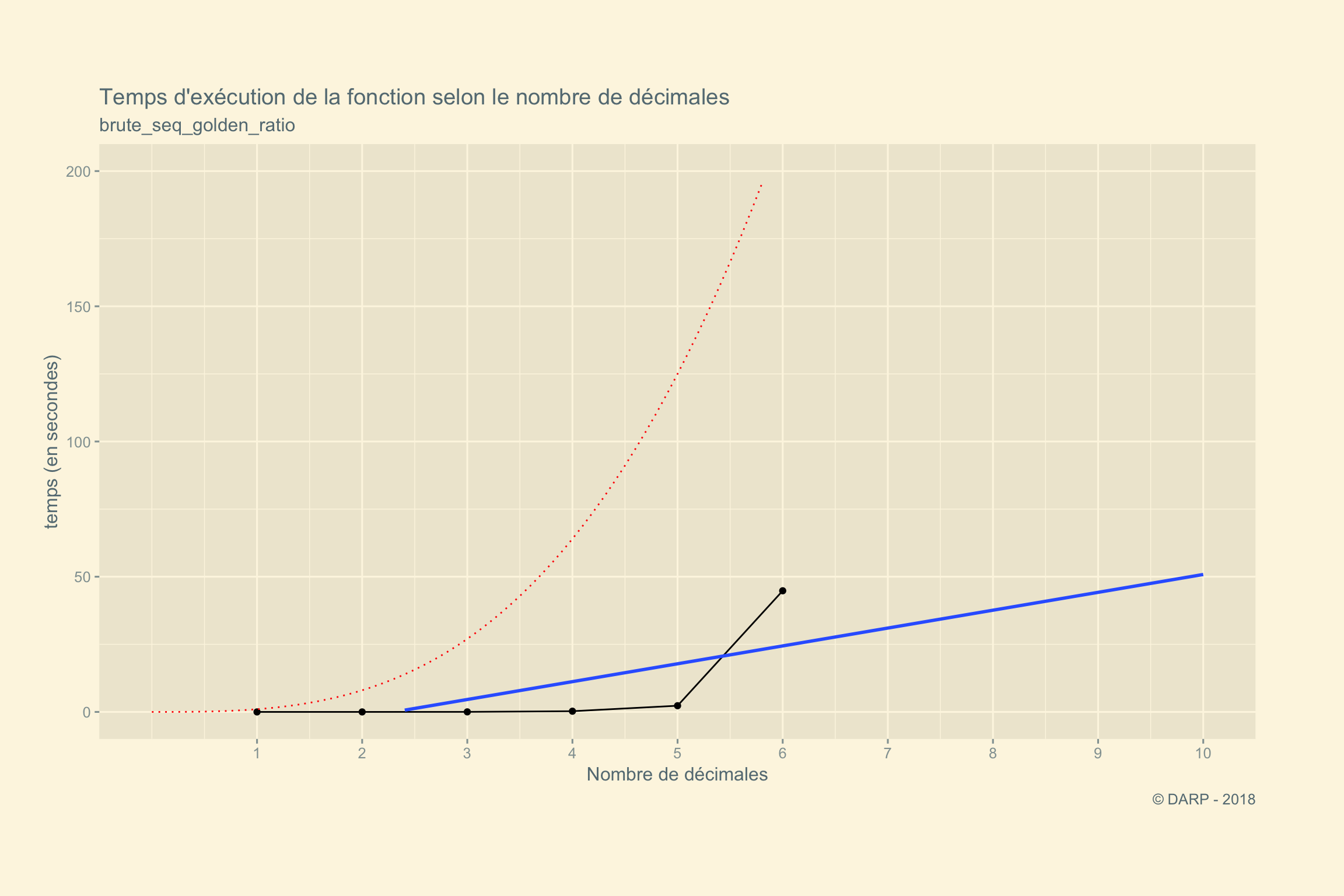
“Brute Force” avec des nombres aléatoires
Nous allons ici tenter de résoudre cette équation par des nombres aléatoires. Le principe est de déterminer une série de nombres dans un intervalle défini à l’avance. Nous savons que la valeur du nombre d’Or nous donne un résultat qui tend vers 0. Chaque valeur alléatoire pour \(x\) nous donnera un résultat donné négatif ou positif. Rien qu’en regardant le graphique nous savons que notre valeur de \(\varphi\) se situe entre 1 et 2. Un nombre en dessous de la valeur réelle de \(\varphi\) nous donnera un résultat négatif pour \(y\), une valeur au-dessus nous donnera un résultat positif. Dès lors pour chaque itération nous conserverons les valeurs \(y\) positives et négatives les plus proches de 0. Ces 2 valeurs définiront l’intervalle suivant et une nouvelle série de nombres aléatoires sera définie.
La fonction définira une “list” inter.val.plot des nombres aléatoires pour réaliser un graphique.
brute_random_golden_ratio <- function(iteration, r.min, r.max, rndm, decimal) {
i <- iteration
x0 <- r.min
x1 <- r.max
dec <- decimal
seq <- c(1:i)
gr.formula <- as_mapper(~ (.x^2 - .x - 1))
inter.val.plot <- list()
for(i in seq) {
inter.val <- runif(rndm, x0, x1)
inter.val.plot[[i]] <- list(inter.val)
inter.val.plot[[i]] <- set_names(inter.val.plot[[i]], paste0("iteration_", i))
table <- inter.val %>%
as_tibble() %>%
mutate(result = gr.formula(value))
result.x0 <- table %>%
filter(result < 0) %>%
filter_at(vars(value), any_vars(. == max(.))) %>%
pull(result)
x0 <- table %>%
filter(result < 0) %>%
filter_at(vars(value), any_vars(. == max(.))) %>%
pull(value)
result.x1 <- table %>%
filter(result > 0) %>%
filter_at(vars(value), any_vars(. == min(.))) %>%
pull(result)
x1 <- table %>%
filter(result > 0) %>%
filter_at(vars(value), any_vars(. == min(.))) %>%
pull(value)
if(round(result.x1, dec) == 0) {
print(paste("iteration # -", i, ": Le nombre d'or se situe entre", round(x0, dec), "et", round(x1, dec)))
inter.val.plot.list <<- inter.val.plot
break
} else {
print(paste("iteration # -", i, "reduction de l'intervalle entre :", x0, "et", x1))
}
}
}Testons la fonction :
set.seed(123)
brute_random_golden_ratio(iteration = 20, r.min = 0, r.max = 2, rndm = 2000, decimal = 12)## [1] "iteration # - 1 reduction de l'intervalle entre : 1.61722408980131 et 1.61869255034253"
## [1] "iteration # - 2 reduction de l'intervalle entre : 1.61803217962116 et 1.61803424409547"
## [1] "iteration # - 3 reduction de l'intervalle entre : 1.61803398856915 et 1.6180339901892"
## [1] "iteration # - 4 reduction de l'intervalle entre : 1.6180339887489 et 1.61803398875074"
## [1] "iteration # - 5 : Le nombre d'or se situe entre 1.61803398875 et 1.61803398875"Il faudra 5 itérations pour trouver le Nombre d’Or ! La fonction est très rapide ! Voyons ce qui se passe graphiquement. Pour cela nous allons récupérer notre list générée par la fonction. Nous appliquons la fonction map_dfc + pluck. pluck permet d’extraire chaque section. Grâce à map_dfc nous obtenons en sortie une table avec chaque section de la liste en colonne. À la suite, nous transformerons la table en table tidy pour avoir l’ensemble des valeurs sur 1 seule colonne.
inter.val.plot.df <- map_dfc(inter.val.plot.list, pluck)
inter.val.plot.df <-
inter.val.plot.df %>%
rowid_to_column()
tidyplot.df <- gather(inter.val.plot.df, iteration, value, -rowid)
head(tidyplot.df, 10)## # A tibble: 10 x 3
## rowid iteration value
## <int> <chr> <dbl>
## 1 1 iteration_1 0.575
## 2 2 iteration_1 1.58
## 3 3 iteration_1 0.818
## 4 4 iteration_1 1.77
## 5 5 iteration_1 1.88
## 6 6 iteration_1 0.0911
## 7 7 iteration_1 1.06
## 8 8 iteration_1 1.78
## 9 9 iteration_1 1.10
## 10 10 iteration_1 0.913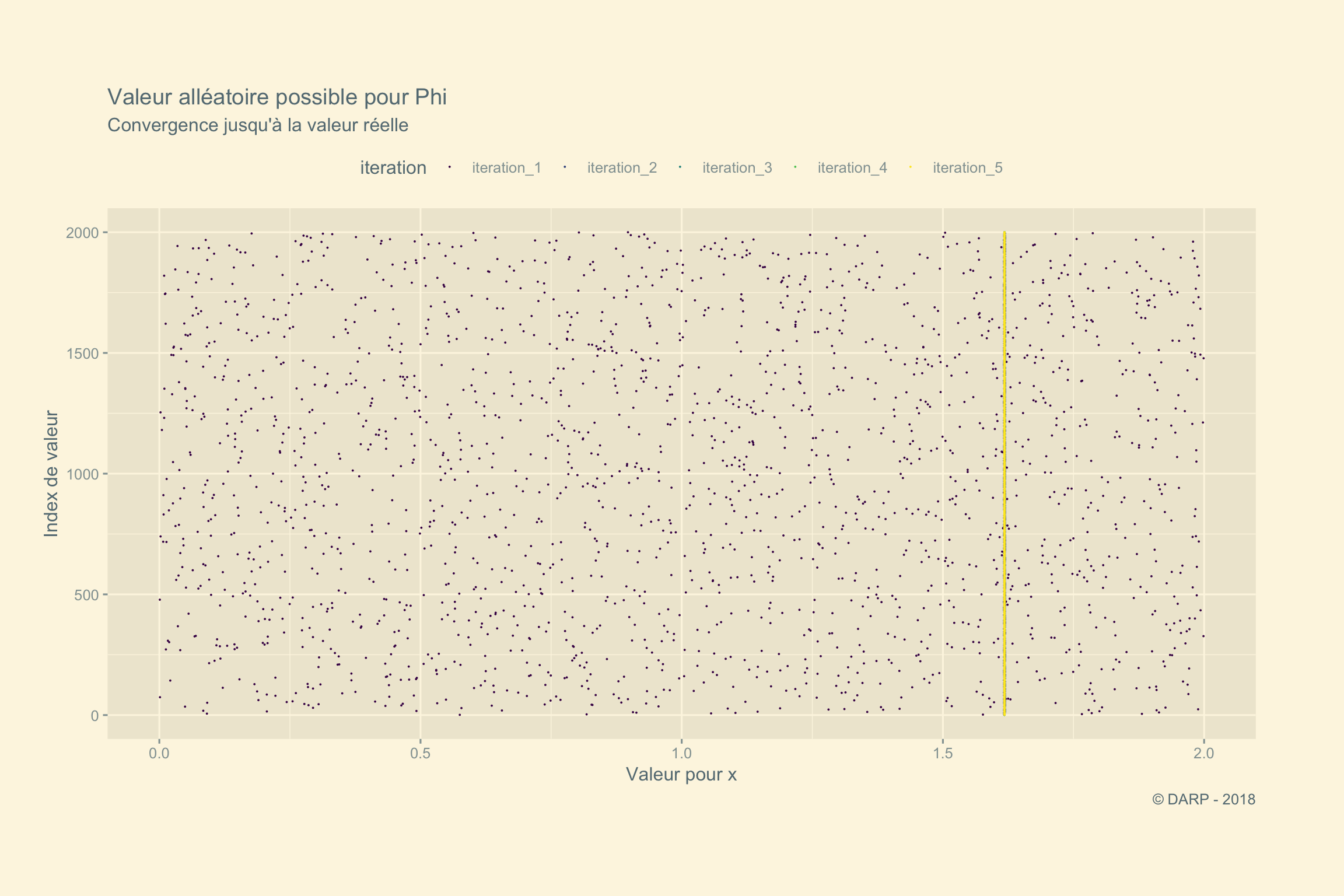
Zoomons un rien entre 1.617et 1.619. Nous voyons le nouvel intervalle lors de l’itération 2 en bleu.
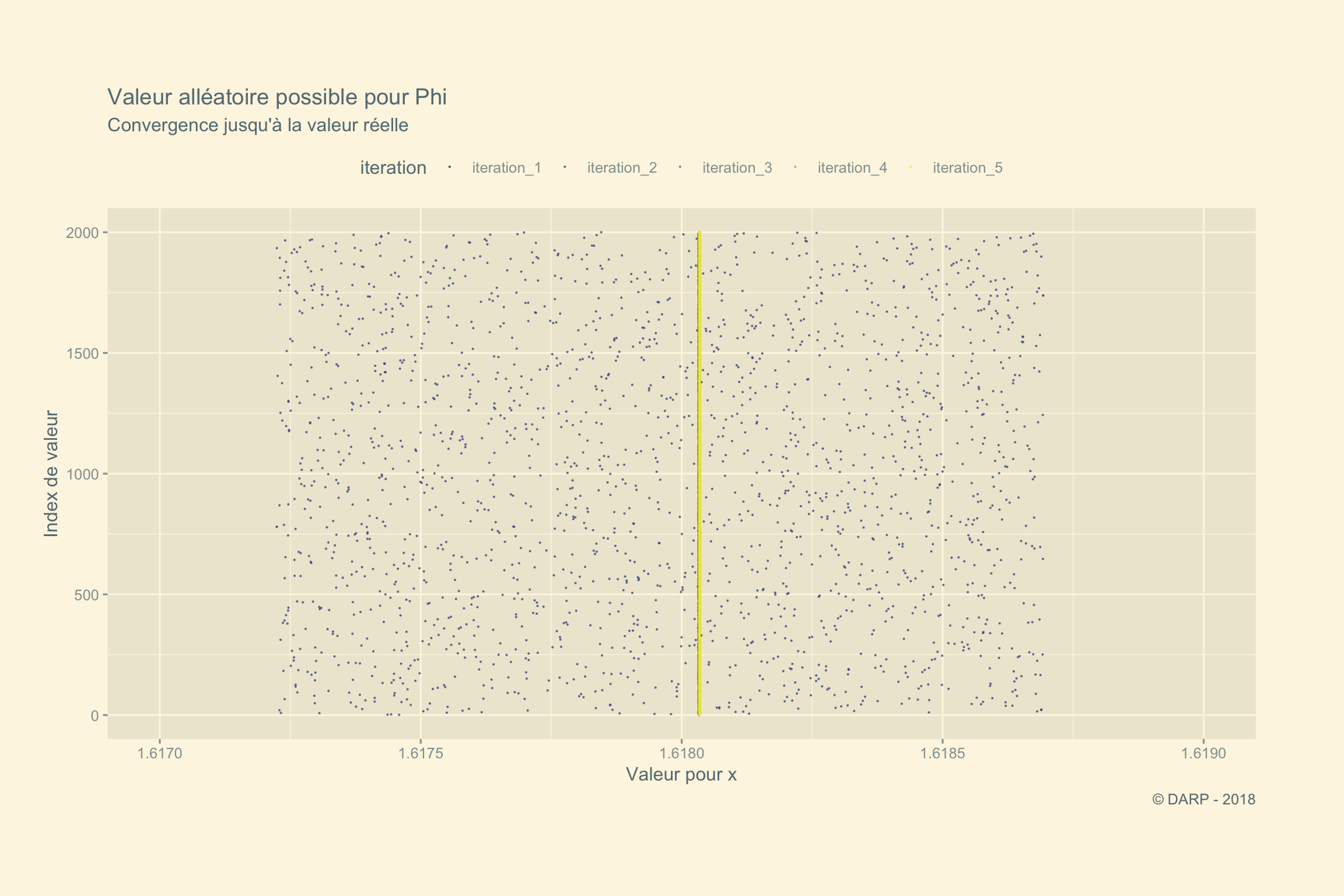
Une petite animation pour terminer cet article en beauté :-)
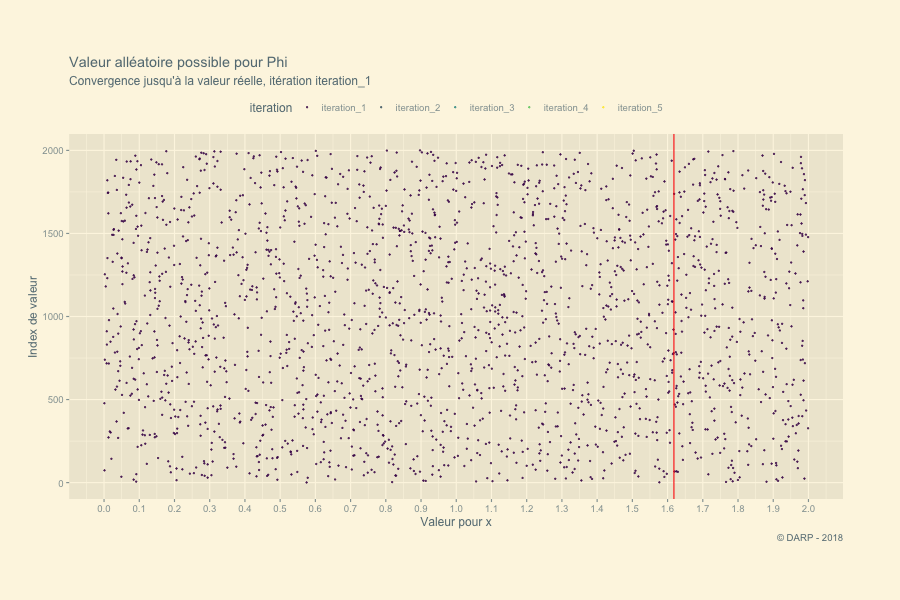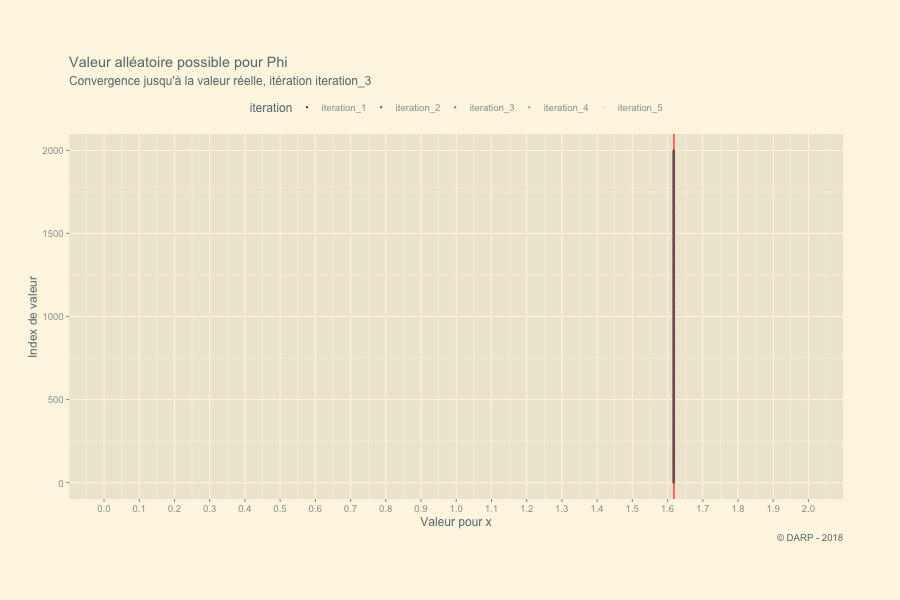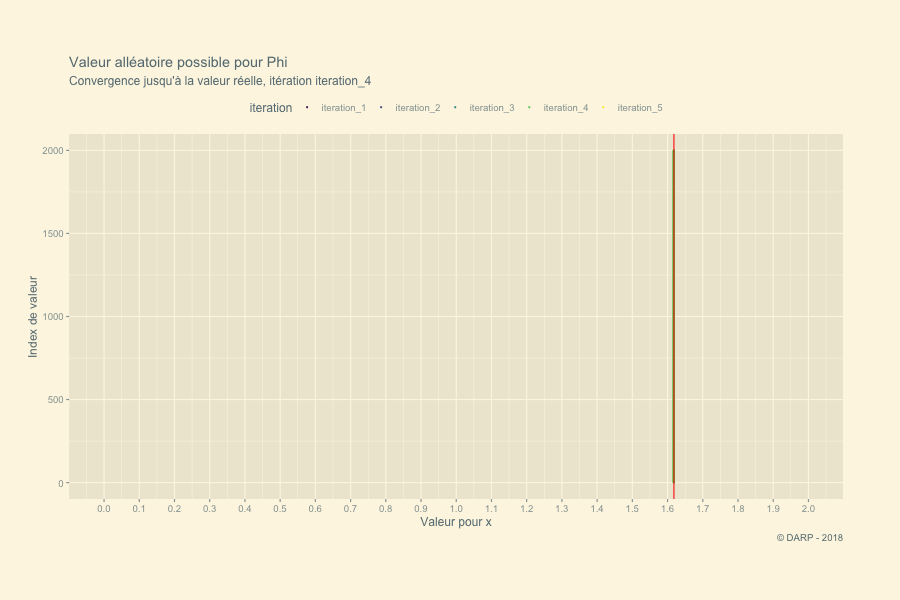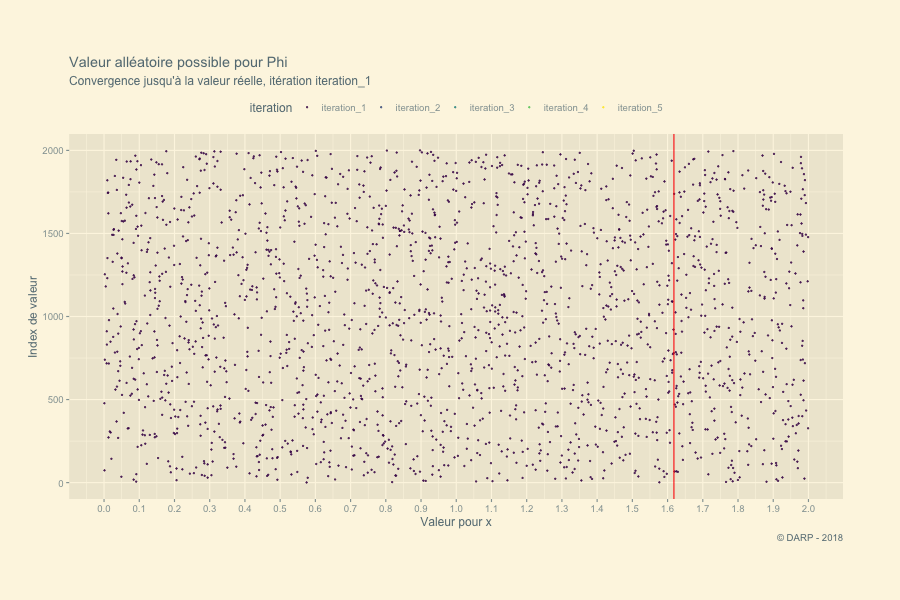
p <- tidyplot.df %>%
ggplot() +
aes(value, rowid, group = iteration, col = iteration) +
geom_point(size = 0.3, alpha = 0.7) +
geom_vline(xintercept = 1.61803398875, col = "red") +
ggthemes::theme_solarized_2() +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
scale_color_viridis_d()+
scale_x_continuous(breaks = seq(0,2, 0.1)) +
labs(title = paste("Valeur alléatoire possible pour Phi"),
subtitle = "Convergence jusqu'à la valeur réelle, itération {closest_state}",
x = "Valeur pour x",
y = "Index de valeur",
caption = "© DARP - 2018") +
gganimate::transition_states(iteration, 30, 4, wrap = TRUE) +
gganimate::ease_aes('exponential-in-out') +
gganimate::enter_fade() +
gganimate::exit_fade()“la mathématique est l’art de donner le même nom à des choses différentes” - Henri Poincaré