L’evolution de prix du gasoil de chauffage et routier au Luxembourg

Reading time ~5 minutes ->
En cette période de l’année, la consommation de mazout de gasoil de chauffage est au maximum. Je me demandais comment était l’évolution du prix à la consommation ces dernières années. Pour aller un peu plus loin, je vais comparer le prix au gasoil routier et voir si l’écart entre les 2 valeurs est constant.
Commençons par télécharger les données sur le site de la Statec. Les 2 fichiers sont téléchargés en “.csv”.
Chargement de tidyverse
Le package tidyverse comprend l’ensemble des libraires nécessaire à l’exploration de données. Le package lubridate comprend des fonctions utiles pour la transformation de dates. Le package ggthemes ajoute des thèmes à ggplot.
library(tidyverse)
library(lubridate)
library(ggthemes)Lecture des csv
Le fichier csv comprend pour la colonne des dates quelques codes. Ils seront ignorés lors du parsing. Commençons par le fichier du gasoil routier.
g.routier <- read_csv("data/e5302.csv",
col_types = cols(Mesures = col_date(format = "%d.%m.%Y"),
`Prix par litre` = col_double())
)Répliquons la manipulation pour le gasoil de chauffage.
g.chauffage <- read_csv("data/e5303.csv",
col_types = cols(Mesures = col_date(format = "%d.%m.%Y"),
`Prix par litre` = col_double())
)Appliquons la fonction glimpse pour les deux bases de données :
glimpse(g.chauffage)## Observations: 823
## Variables: 2
## $ Mesures <date> NA, 2018-12-21, 2018-12-14, 2018-11-29, 2018...
## $ `Prix par litre` <dbl> NA, 0.579, 0.604, 0.623, 0.649, 0.684, 0.700,...glimpse(g.routier)## Observations: 730
## Variables: 2
## $ Mesures <date> NA, 2018-12-21, 2018-12-05, 2018-11-29, 2018...
## $ `Prix par litre` <dbl> NA, 1.057, 1.084, 1.099, 1.119, 1.149, 1.162,...823 observations pour le chauffage, 730 pour le gasoil routier.
Data Cleaning et préparation
Nous avons dans une même année plusieurs références de prix. C’est surtout l’évolution qui nous intéresse et moins la volatilité sur l’année. Je vais donc calculer la moyenne des prix par année pour ne garder qu’une seule valeur. Nous appliquons les fonctions suivantes :
- Supppression des NA
- Renommer les noms de colonnes
- Transformer la colonne
dateen année
- Calculer la moyenne par an et arrondissement à 3 décimales
- Ne garder qu’une seule référence par année
g.routier2 <-
g.routier %>%
filter_all(all_vars(!is.na(.))) %>%
rename(date = "Mesures", price_gr = "Prix par litre") %>%
mutate(year = year(date)) %>%
group_by(year) %>%
mutate(routier = round(mean(price_gr), 3)) %>%
select(year, routier) %>%
unique()g.chauffage2 <-
g.chauffage %>%
filter_all(all_vars(!is.na(.)))%>%
rename(date = "Mesures", price_gc = "Prix par litre") %>%
mutate(year = year(date))%>%
group_by(year) %>%
mutate(chauffage = round(mean(price_gc), 3)) %>%
select(year, chauffage) %>%
unique()Voici le résultat.
head(g.routier2, 15)## # A tibble: 15 x 2
## # Groups: year [15]
## year routier
## <dbl> <dbl>
## 1 2018 1.09
## 2 2017 0.991
## 3 2016 0.913
## 4 2015 1.01
## 5 2014 1.15
## 6 2013 1.22
## 7 2012 1.26
## 8 2011 1.16
## 9 2010 0.992
## 10 2009 0.844
## 11 2008 1.18
## 12 2007 0.932
## 13 2006 0.925
## 14 2005 0.835
## 15 2004 0.706head(g.chauffage2, 15)## # A tibble: 15 x 2
## # Groups: year [15]
## year chauffage
## <dbl> <dbl>
## 1 2018 0.64
## 2 2017 0.535
## 3 2016 0.449
## 4 2015 0.529
## 5 2014 0.7
## 6 2013 0.768
## 7 2012 0.817
## 8 2011 0.734
## 9 2010 0.586
## 10 2009 0.451
## 11 2008 0.703
## 12 2007 0.546
## 13 2006 0.532
## 14 2005 0.487
## 15 2004 0.381Calcul de l’erreur standard (se) de la moyenne et de l’intervalle de confiance.
La variation de prix sur une année peut être grande. Nous allons donc calculer l’intervale de confiance à 95% de la moyenne et l’utiliser sur nos graphiques à venir. Petit rappel statistique :
- la Moyenne :
m = [(x1 + x2 +...+ (xn)] / noumean(); - la Médiane :
(n + 1)/2oumedian();
- la Variance :
s2 = [(x1 – m)2 + (x2 – m)2 +...+ (xn–m)2] / (n – 1)ouvar();
- l’Ecart-type (Standard Deviation) :
sqrt(s2)ousd(); - l’Erreur Standard (s.e.) :
sd / sqrt(n);
- l’intervalle de confiance à 95 % :
μ = m +/- 1.96 * se
Merci à @brodriguesco pour sa rectification sur le calcul de l’intervalle de confiance. Nous allons également ajouter l’étendue pour chaque année, nous pourrons ainsi comparer les 2 graphiques générés.
g.routier3 <-
g.routier %>%
filter_all(all_vars(!is.na(.))) %>%
rename(date = "Mesures", price_gr = "Prix par litre") %>%
mutate(year = year(date)) %>%
group_by(year) %>%
mutate(route = round(mean(price_gr), 3),
var = var(price_gr),
se = sd(price_gr)/sqrt(n()),
ic95n_r = route - (1.96 * se),
ic95p_r = route + (1.96 * se),
minp_r = min(price_gr),
maxp_r = max(price_gr)) %>%
select(year, route, ic95n_r, ic95p_r, minp_r, maxp_r) %>%
unique()g.chauffage3 <-
g.chauffage %>%
filter_all(all_vars(!is.na(.))) %>%
rename(date = "Mesures", price_gc = "Prix par litre") %>%
mutate(year = year(date)) %>%
group_by(year) %>%
mutate(chauffage = round(mean(price_gc), 3),
var = var(price_gc),
se = sd(price_gc)/sqrt(n()),
ic95n_c = chauffage - (1.96 * se),
ic95p_c = chauffage + (1.96 * se),
minp_c = min(price_gc),
maxp_c = max(price_gc)) %>%
select(year, chauffage, ic95n_c, ic95p_c, minp_c, maxp_c) %>%
unique()Jointure des données
Nous allons joindre les données de façon à n’avoir qu’une seule base de données. Nous manipulerons aussi la base de données afin d’avoir toutes les variables par colonnes. C’est la transformation tidy. Pour plus d’information sur les tidy data vous pouvez consulter l’article de Hadley Wickham ici : tidy data.
Nous appliquons la fonction inner_join pour ne garder que les observations disponibles par années dans les 2 bases de données. Nous nommerons la nouvelle base de données gasoil.
gasoil <- inner_join(g.chauffage3, g.routier3, by = "year")
tidy_gas <- gather(gasoil, key = type, value = price, -c(year, ic95n_c, ic95p_c, ic95n_r, ic95p_r, minp_r, maxp_r, minp_c, maxp_c))voici le résultat.
tidy_gas %>%
filter(year == 2008)## # A tibble: 2 x 11
## # Groups: year [1]
## year ic95n_c ic95p_c minp_c maxp_c ic95n_r ic95p_r minp_r maxp_r type
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 2008 0.659 0.747 0.374 0.893 1.07 1.29 0.789 2.34 chau…
## 2 2008 0.659 0.747 0.374 0.893 1.07 1.29 0.789 2.34 route
## # ... with 1 more variable: price <dbl>Vérifions les valeurs avec la fonction t.test()sur l’année 2008.
g.chauffage %>%
filter_all(all_vars(!is.na(.))) %>%
mutate(Mesures = year(Mesures)) %>%
group_by(Mesures) %>%
filter(Mesures == 2008) %>%
pull("Prix par litre") %>%
t.test(conf.level = 0.95)##
## One Sample t-test
##
## data: .
## t = 31.151, df = 38, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.6572669 0.7486305
## sample estimates:
## mean of x
## 0.7029487Visualisation des données
Nous allons maintenant afficher le graphique correspondant aux données. Les lignes noires pointilles indiques les années des chocs pétroliers (source wikipedia) :
- 1973 : 1er choc
On parle de « premier choc pétrolier » pour identifier l’augmentation massive du prix du pétrole due en particulier au fait que les États-Unis ont passé leur pic de production en 1971, cela suivi de l’abandon de Bretton Woods et d’une dévaluation du dollar ajoutant à la pression haussière sur le baril (qui provoquera par ricochet l’instabilité monétaire des années 1975-1985) alors que l’embargo arabe lié à la guerre du Kippour d’octobre 1973 jugule l’importation de brut.
- 1979 : 2e choc
Le deuxième choc pétrolier s’est produit en 1979. On parle de « second choc pétrolier » pour qualifier le second cycle de hausses des prix. Sous les effets conjugués de la Révolution iranienne, de la fuite du Shah et de la guerre Iran-Irak, le prix du pétrole est multiplié par 2,7 entre la mi-1978 et 1981, ce qui déclenche aux États-Unis la crise monétaire de 1980.
- 2008 : 3e choc
Dans la première partie de l’année 2008, on constate à nouveau une envolée surprise des prix du pétrole, le baril atteignant 147 dollars pour ensuite replonger brutalement à la fin de 2008 et au début de 2009, atteignant un creux de 40 dollars avant de rebondir. Ce choc pétrolier fut essentiellement dû à une spéculation débridée, comme le montre, entre autres, l’étude de Masters Capital Management fin 2008.
Préparons les graphiques :
1er graphique
g.routier %>%
arrange(desc(`Prix par litre`))## # A tibble: 730 x 2
## Mesures `Prix par litre`
## <date> <dbl>
## 1 2008-09-04 2.34
## 2 2008-09-25 2.31
## 3 2008-09-19 2.25
## 4 2012-10-13 1.33
## 5 2012-08-22 1.32
## 6 2012-08-14 1.31
## 7 2012-09-12 1.30
## 8 2012-10-03 1.3
## 9 2008-08-02 1.30
## 10 2012-10-19 1.29
## # ... with 720 more rowstidy_gas %>%
ggplot() +
aes(year, price, ic95n_c, ic95p_c) +
geom_ribbon(aes(x = year, ymax = maxp_c, ymin = minp_c, width = 0.3), fill = "coral4", alpha = 0.35) +
geom_errorbar(aes(x = year, ymax = ic95p_c, ymin = ic95n_c, width = 0.3), fill = "coral4", alpha = 0.5) +
geom_ribbon(aes(x = year, ymax = maxp_r, ymin = minp_r, width = 0.3), fill = "slategray4", alpha = 0.35) +
geom_errorbar(aes(x = year, ymax = ic95p_r, ymin = ic95n_r, width = 0.3), fill = "slategray4", alpha = 0.5) +
geom_line(aes(col = type)) +
geom_point(col = "black", size = 0.7, alpha = 0.4) +
geom_smooth(se = FALSE, linetype = 4, size = 0.8, aes(col = type)) +
geom_vline(xintercept = c(1973, 1979, 2008), linetype = 1, col = "orange3", alpha = 0.6) +
annotate(x= 1973, y = 2, geom = "label", label = "1er choc", fill = "orange2", col = "white", size = 4, label.padding = unit(0.35, "lines")) +
annotate(x= 1979, y = 2, geom = "label", label = "2e choc", fill = "orange2", col = "white", size = 4, label.padding = unit(0.35, "lines")) +
annotate(x= 2008, y = 2, geom = "label", label = "3e choc", fill = "orange2", col = "white", size = 4, label.padding = unit(0.35, "lines")) +
annotate(x= 1990, y = 0.8, geom = "label", label = "Guerre du Golfe, 1990", size = 3) +
annotate("point", y = 2.341, x = 2008, col = "red4", size = 2) +
annotate("text", y = 2.341, x = 2008, label = "2.341 EUR, 04.09.2008", col = "red4", size = 3, hjust = -0.1) +
theme_solarized_2() +
scale_y_continuous(limits = c(0, 2.4)) +
scale_x_continuous(breaks = seq(1960, 2020, by = 5), minor_breaks = seq(1960, 2020, by = 1)) +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
labs(title = "Prix du gasoil routier et de chauffage au Luxembourg",
x = "Années",
y = "Prix moyen en Euro, IC 95%, étendue : min & max",
subtitle = "1965 - 2018",
caption = " © DARP - Données Statec - 2018")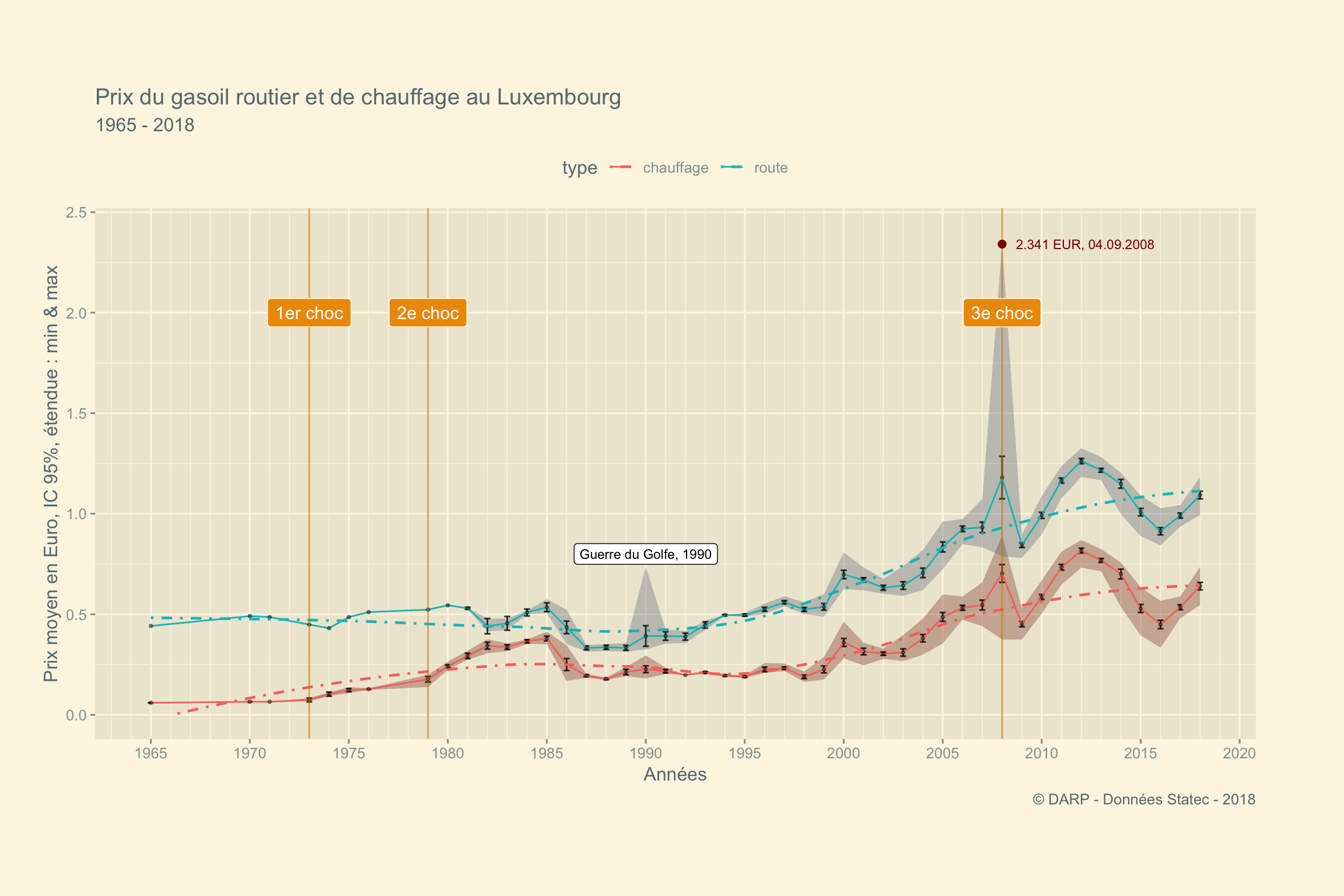
Calculons la différence de prix entre les 2 types et leur valeur moyenne. Nous observons que c’est en 1982 que la différence entre les 2 types de gasoil était la plus faible. Nous voyons sur ce graphique allégé la progression de l’écart entre les 2 valeurs.
tidy_gas %>%
ggplot() +
aes(year, price, ic95n_c, ic95p_c) +
geom_smooth(se = FALSE, linetype = 4, size = 0.8, aes(col = type)) +
theme_solarized_2() +
scale_y_continuous(limits = c(0, 2)) +
scale_x_continuous(breaks = seq(1960, 2020, by = 5), minor_breaks = seq(1960, 2020, by = 1)) +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
labs(title = "Prix du gasoil routier et de chauffage au Luxembourg - régression polynomiale",
x = "Années",
y = "Prix moyen en Euro",
subtitle = "1965 - 2018",
caption = " © DARP - Données Statec - 2018")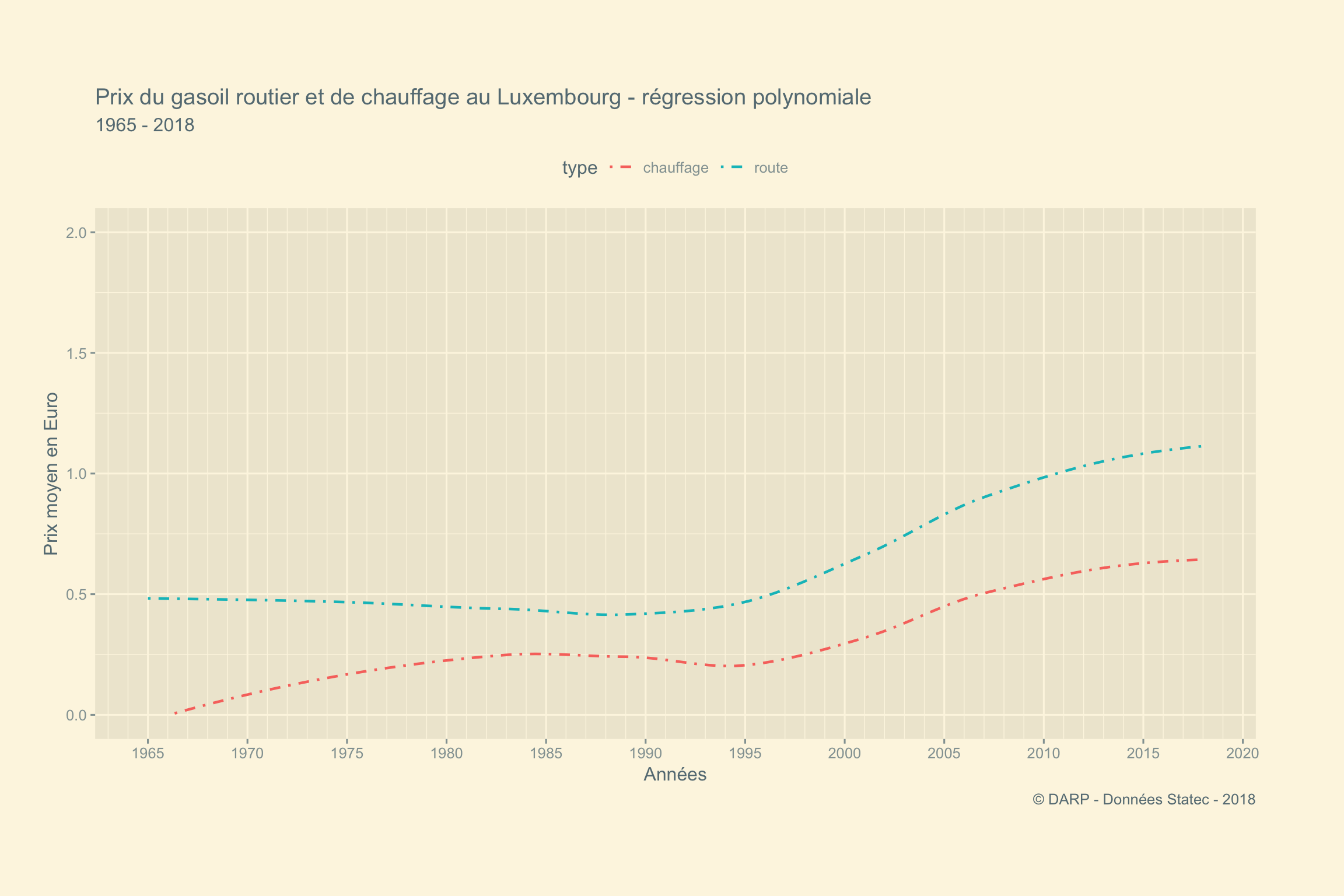
gasoil %>%
mutate(diff = route - chauffage) %>%
select(year, diff) %>%
arrange(diff)## # A tibble: 47 x 2
## # Groups: year [47]
## year diff
## <dbl> <dbl>
## 1 1982 0.097
## 2 1983 0.118
## 3 1989 0.12
## 4 1987 0.138
## 5 1984 0.143
## 6 1985 0.155
## 7 1988 0.157
## 8 1990 0.165
## 9 1991 0.175
## 10 1986 0.185
## # ... with 37 more rowsObservons l’évolution de cette différence sur les années.
- En rouge : la différence en €
- En pointillé noir : la moyenne de cette différence, soit
0.319€
gasoil %>%
mutate(diff = route - chauffage) %>%
ungroup() %>%
mutate(m = mean(diff)) %>%
select(year, diff, m) %>%
ggplot() +
aes(year, diff, m) +
geom_line(col = "red") +
geom_point(col = "red3") +
geom_hline(yintercept = 0.319, linetype = 2, size = 0.4 ) +
theme_solarized_2() +
scale_y_continuous(limits = c(0, 2)) +
scale_x_continuous(minor_breaks = seq(1960, 2020, by = 1)) +
theme(legend.position = "top", plot.margin = unit(c(2,2,2,1), "cm")) +
labs(title = "Ecart de prix entre le gasoil routier et de chauffage au Luxembourg",
x = "Années",
y = "Difference en Euro (moyenne par année)",
subtitle = "1965 - 2018",
caption = " © DARP - Données Statec - 2018")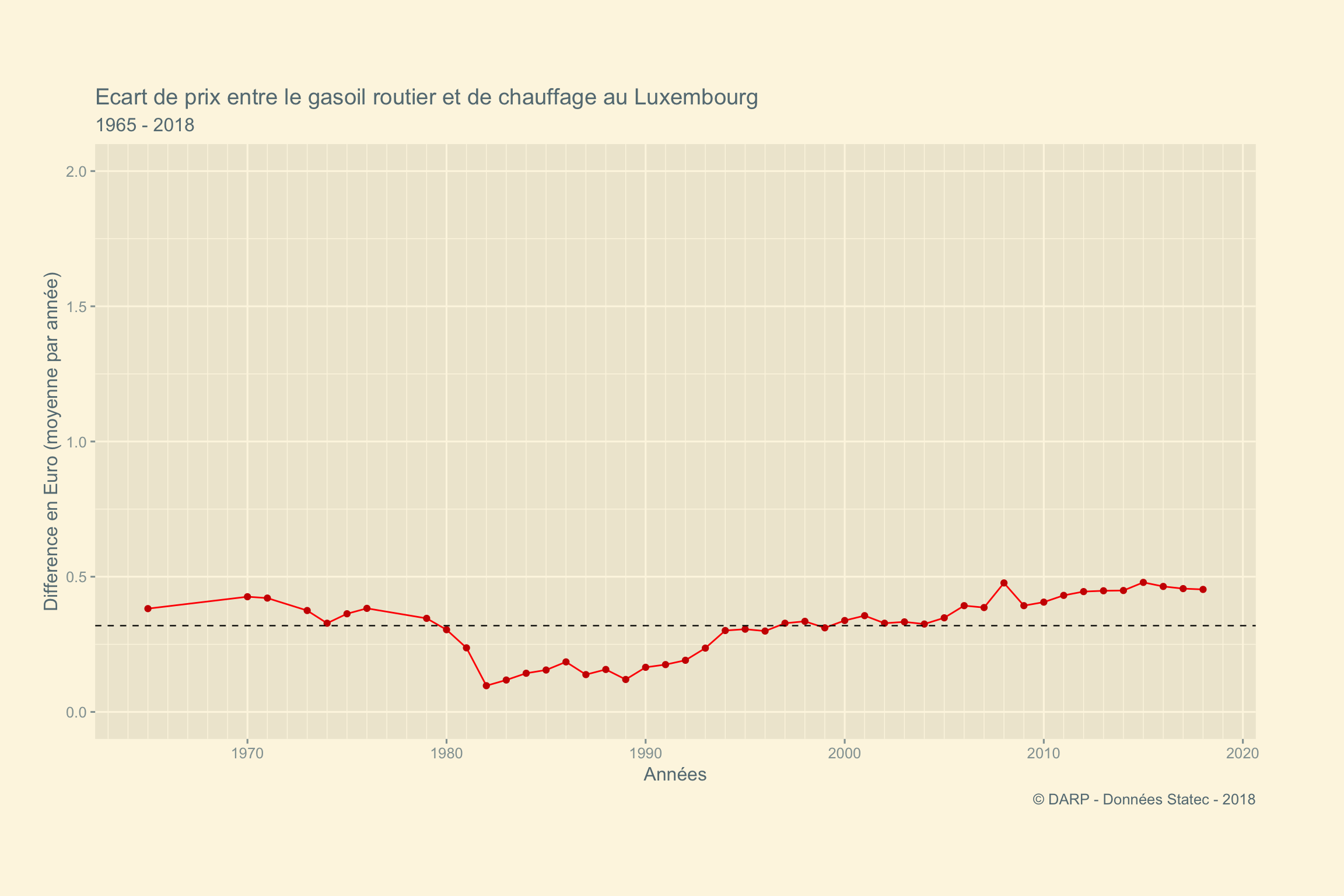
Nous pouvons donc observer une augmentation de l’écart de prix depuis les années 1982 même si les prix du gasoil routier et de chauffage suivent une même courbe de progression.