Les données abberantes du CIM

Reading time ~ 10 minutes ->
L’objectif de cet article est d’identifier sur la semaine ou sur le mois, les journées où les sessions sont anormalement élevées. Plusieurs méthodes nous permettent d’identifier les outliers soit les valeurs aberrantes. Je pense notatement au calcul de centiles ou via le z-score (Cote Z). Existe’-il une méthode robuste? Nous testerons différentes solutions. Première étape, le chargement des datas avec readRDS.
cim <- readRDS("data/cim_db_shiny_31012019.rds")Approche 1 : Identification par les centiles.
Nous allons observer uniquement les sessions pour l’instant. Réalisons le premier graphique. le package ggridges comprend une fonction pour faciliter la visualisation des courbes de distribution (Density plot). Le paramètre quantiles_lines permet le représentation de quantiles. Fixons les quantiles à 0.05 et 0.95.
cim %>%
filter(metrics == "sessions") %>%
ggplot() +
aes(hits, site, fill = ..y..) +
geom_density_ridges2(aes(), scale = 2, quantile_lines = TRUE, quantiles = c(0.05, 0.95), alpha = 0.9)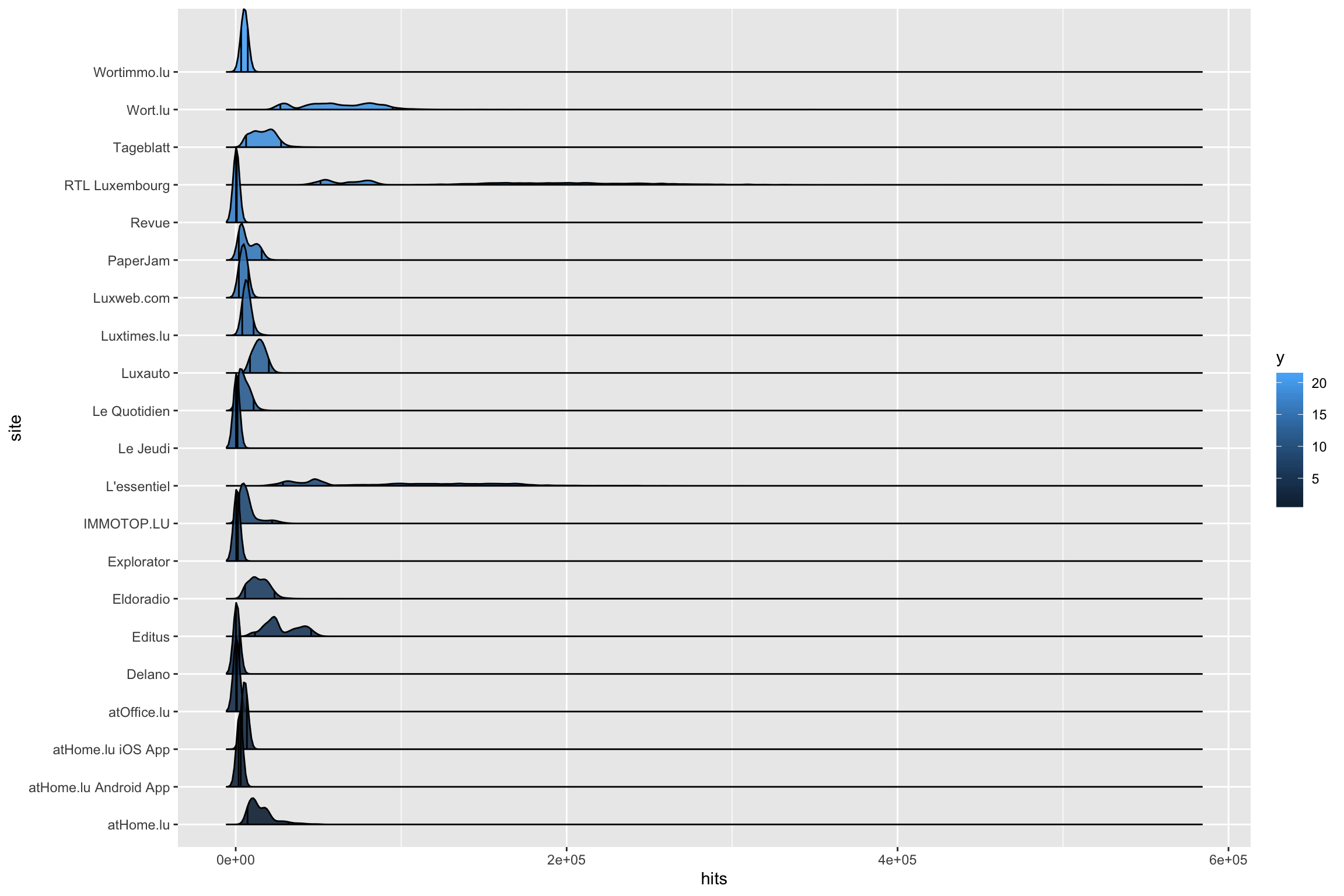
Les valeurs élevées de L'essentiel et de RTL rendent la comparaison assez difficile. En effet l’échelle des x couvre une grande étendue.
Pour rappel, nous essayons d’identifier les jours où le nombre de sessions est anormal. Pouvons-nous le faire en identifiant les sessions dont le nombre de sessions est au-delà du 95e centile?
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg", "L'essentiel", "Wort.lu")) %>%
ggplot() +
aes(hits, site, fill = ..y..) +
geom_density_ridges2(aes(), scale = 2, quantile_lines = TRUE, quantiles = c(0.05, 0.95), alpha = 0.9)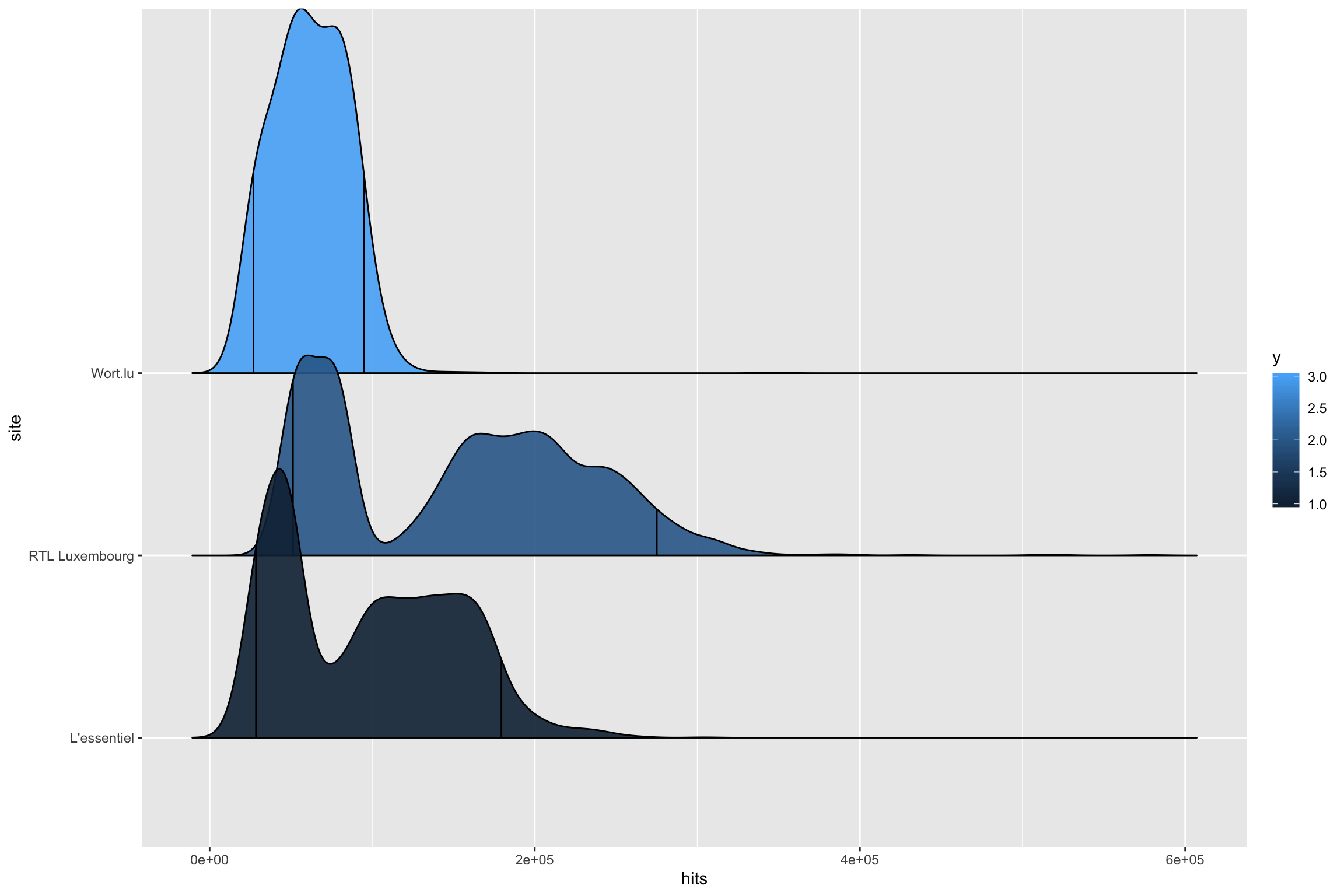
On voit sur ce graphique de manière assez évidente 2 modes pour RTLet L'essentiel. Il s’agit probablement des sessions mesures les jours de la semaine et puis le week-end.
Bon, concentrons-nous sur un site uniquement. Utilisons les semaines de 2018 pour les ordonnées.
Appelons ..quantile.. pour représenter les échelles.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01") %>%
mutate(week = lubridate::week(date)) %>%
ggplot() +
aes(hits, forcats::fct_rev(factor(week)), fill = factor(..quantile..)) +
geom_density_ridges_gradient(scale = 3, quantile_lines = TRUE, quantiles = c(0.05, 0.95)) +
scale_fill_viridis_d()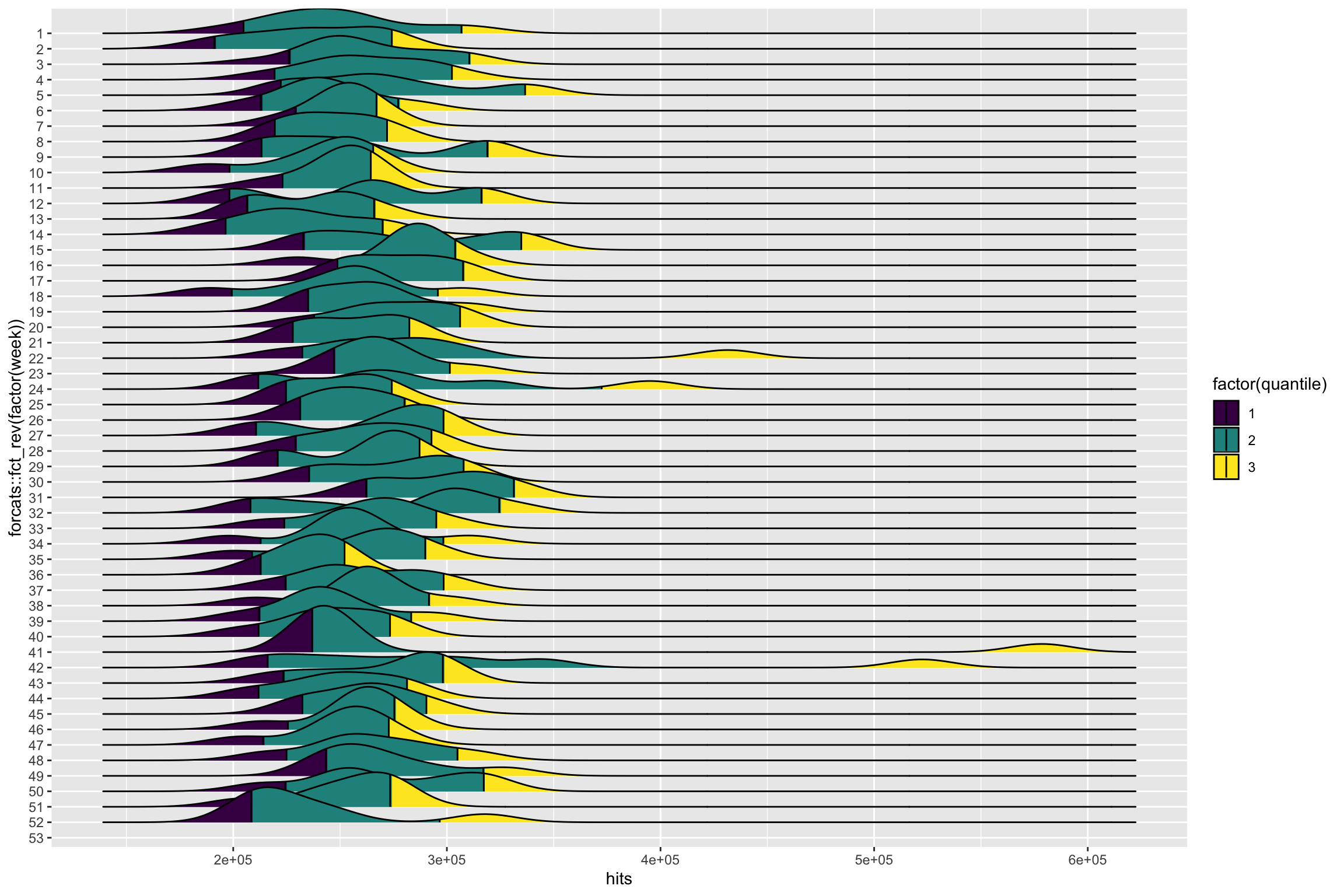
On peut voir effectivement que toutes les semaines, nous pouvons avoir des jours dans le 95e centile. Plusieurs approches sont donc possibles, sur l’ensemble de l’année, par mois ou par semaine. Essayons le même graphique, mais pour chaque mois.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01") %>%
mutate(month = lubridate::month(date)) %>%
ggplot() +
aes(hits, forcats::fct_rev(factor(month)), fill = factor(..quantile..)) +
geom_density_ridges_gradient(scale = 2, quantile_lines = TRUE, quantiles = c(0.05, 0.95)) +
scale_fill_viridis_d()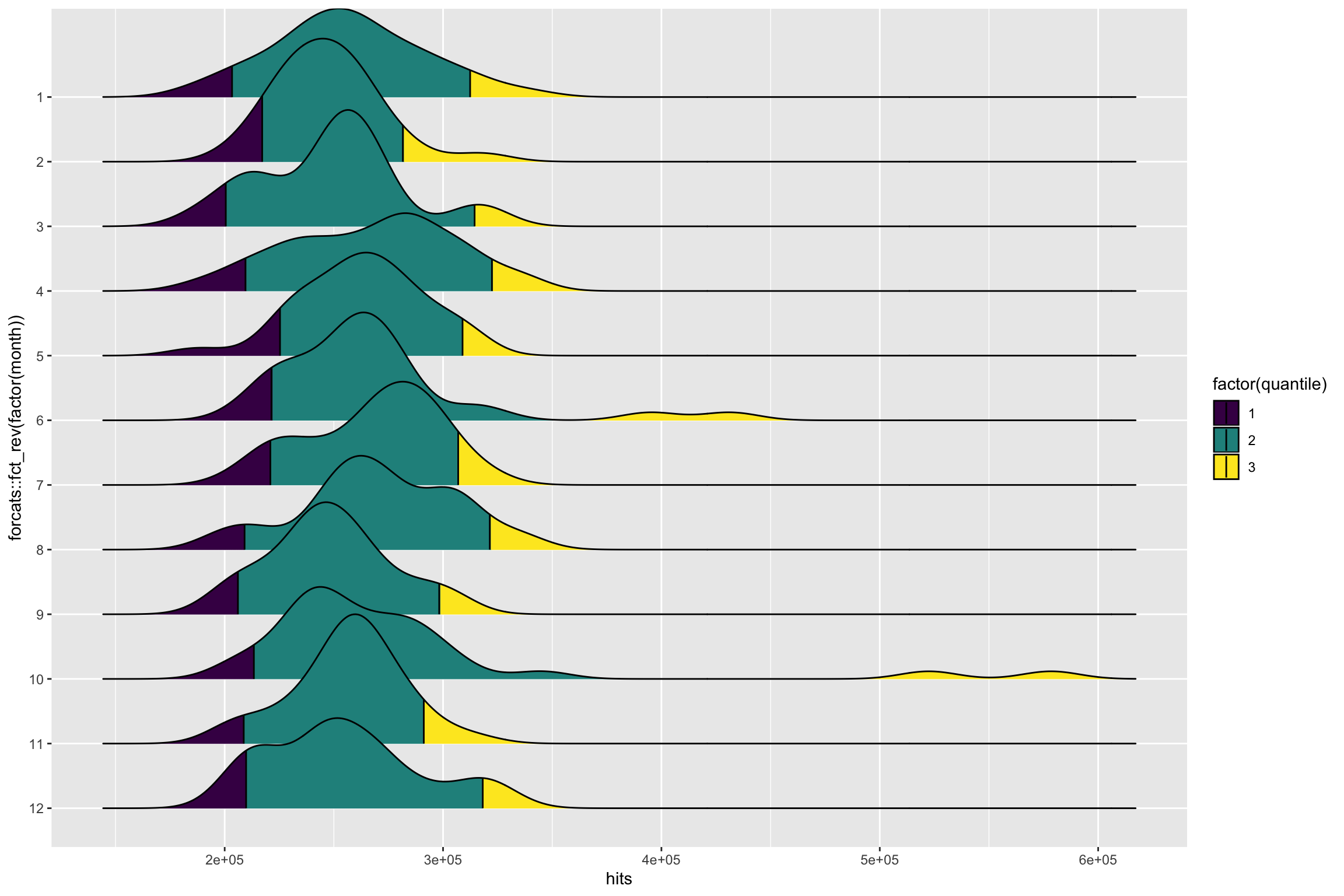
Il est évident que suivant le nombre de dates que nous souhaitons identifier, il faudra choisir l’intervalle.
C’est-à-dire que le nombre de dates sera > que l’intervalle choisi (1 an, 12 mois, 52 semaines). Étant donné que cette time série à une évolution (trends), la valeur des sessions appartenant au quantile souhaité varie avec le temps. Testons la fonction calcPercentile du package openair.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01") %>%
openair::calcPercentile(pollutant = "hits", avg.time = "month",
percentile = 99, data.thresh = 5, start = NA)## date percentile.99
## 1 2018-01-01 294377.9
## 2 2018-02-01 308913.5
## 3 2018-03-01 319241.9
## 4 2018-04-01 334887.2
## 5 2018-05-01 309357.6
## 6 2018-06-01 420902.9
## 7 2018-07-01 317699.4
## 8 2018-08-01 334534.9
## 9 2018-09-01 303468.4
## 10 2018-10-01 561667.5
## 11 2018-11-01 307346.6
## 12 2018-12-01 325115.6
## 13 2019-01-01 338126.6Mouais… En fait, cela revient à prendre pour chaque mois la valeur max… Voyons cela :
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
filter(hits == max(hits)) %>%
arrange(desc(date))## # A tibble: 12 x 5
## # Groups: month [12]
## date site metrics hits month
## <date> <chr> <chr> <dbl> <dbl>
## 1 2019-01-30 RTL Luxembourg sessions 341126 1
## 2 2018-12-03 RTL Luxembourg sessions 327866 12
## 3 2018-11-29 RTL Luxembourg sessions 312577 11
## 4 2018-10-14 RTL Luxembourg sessions 578463 10
## 5 2018-09-10 RTL Luxembourg sessions 303975 9
## 6 2018-08-03 RTL Luxembourg sessions 335632 8
## 7 2018-07-31 RTL Luxembourg sessions 321351 7
## 8 2018-06-01 RTL Luxembourg sessions 431512 6
## 9 2018-05-13 RTL Luxembourg sessions 309510 5
## 10 2018-04-10 RTL Luxembourg sessions 336131 4
## 11 2018-03-02 RTL Luxembourg sessions 319454 3
## 12 2018-02-27 RTL Luxembourg sessions 317729 2Soit 12 dates à examiner. Est-ce que ces 12 dates représentent des dates anormalement hautes? Voyons cela sur un graphique. Sauvegardons les dates dans un vecteur.
cim %>%
arrange(desc(date)) %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
filter(hits == max(hits)) %>%
pull(date) -> high_datecim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
select(date, month, hits) %>%
ggplot() +
aes(date, hits, col = (date %in% high_date)) +
geom_point(size = 2) +
geom_line(aes(group = month)) +
theme(legend.position = "none") +
labs(title = "RTL Luxembourg - Sessions 2018") +
facet_wrap(~month, scales = "free")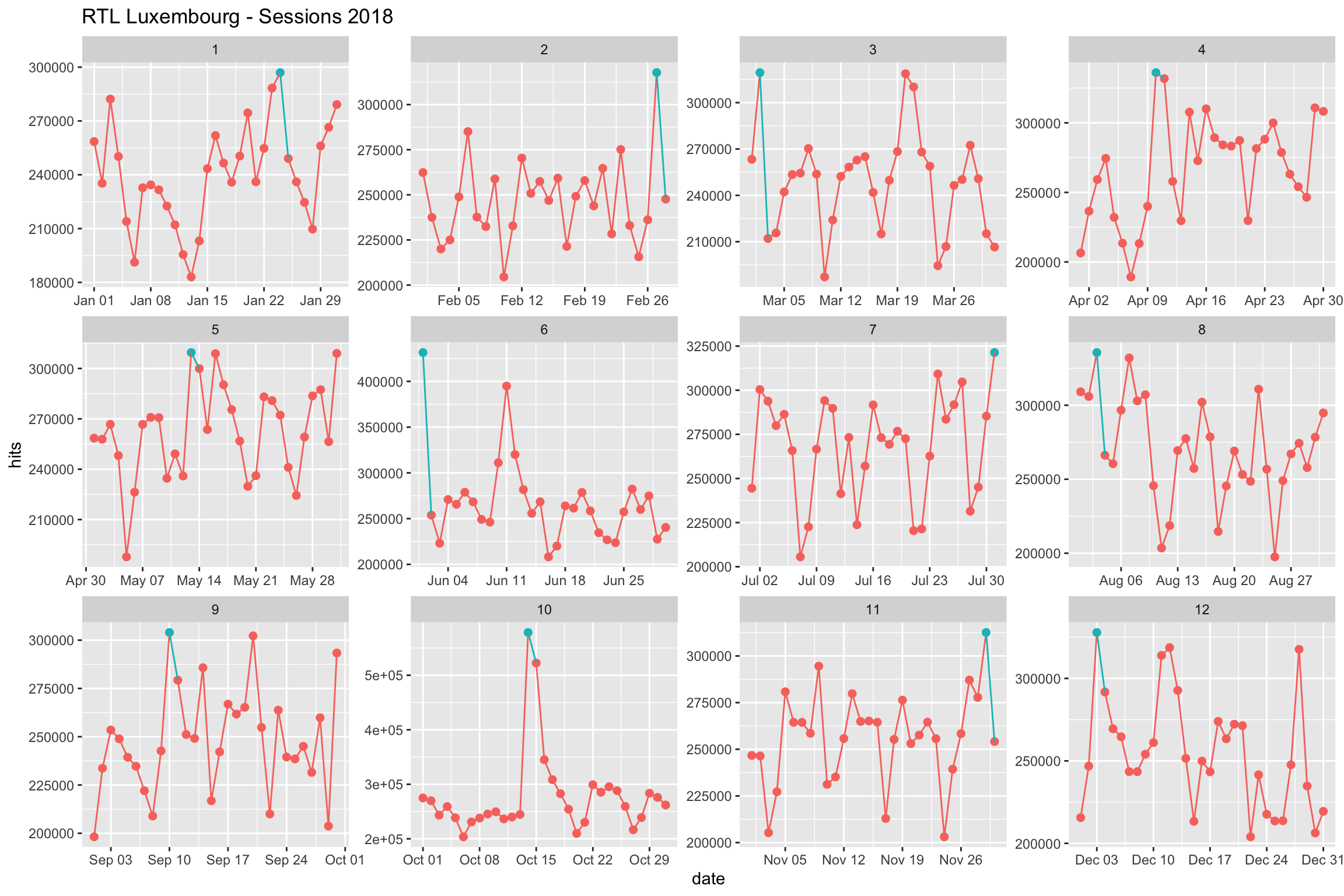
Tout cela ne nous aide pas de trop. Nous voyons bien les jours en bleu où le sessions sont les plus importantes pour chaque mois.
Approche 2 : Règle des 3 sigmas.
Voici ce que nous dit wikipedia :
La règle des trois sigmas exprime une heuristique fréquemment utilisée : la plupart des valeurs se situent a moins de trois fois l’écart-type de la moyenne. Pour de nombreuses applications pratiques, ce pourcentage de 99.3% peut être considéré comme une quasi-certitude. L’usage de cette heuristique dépend cependant du domaine : ainsi en sciences sociales, un résultat est considéré comme significatif si son intervalle de confiance est au moins de 95%, soit de l’ordre de deux sigmas, alors qu’en physique des particules, le seuil de significativité se situe autour de cinq sigmas (soit un intervalle de confiance à 99.99994%).
La règle des trois sigmas est également applicable à d’autres distributions que la loi normale. En effet, l’Inégalité de Bienaymé-Tchebychev permet d’affirmer que pour toute variable aléatoire, au moins 88.8% des réalisations se situent dans un intervalle de trois sigmas.
Ces valeurs numériques (68%, 95% et 99.7%) proviennent de la fonction de répartition de la loi normale.
Ajoutons la moyenne pour chaque mois afin de sélectionner notre référence à laquelle nous ajouterons le calcul de l’écart-type (sd = Standard Deviation en anglais). Nous voulons afficher les dates dont la valeur est supérieure ou inférieure à 3 sigma.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
mutate(mean.month = mean(hits), med.month = median(hits)) %>%
ungroup() %>%
select(date, month, mean.month, med.month, hits) %>%
ggplot() +
aes(date, hits) +
geom_point(size = 3, alpha = .4) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
facet_wrap(~month, scales = "free")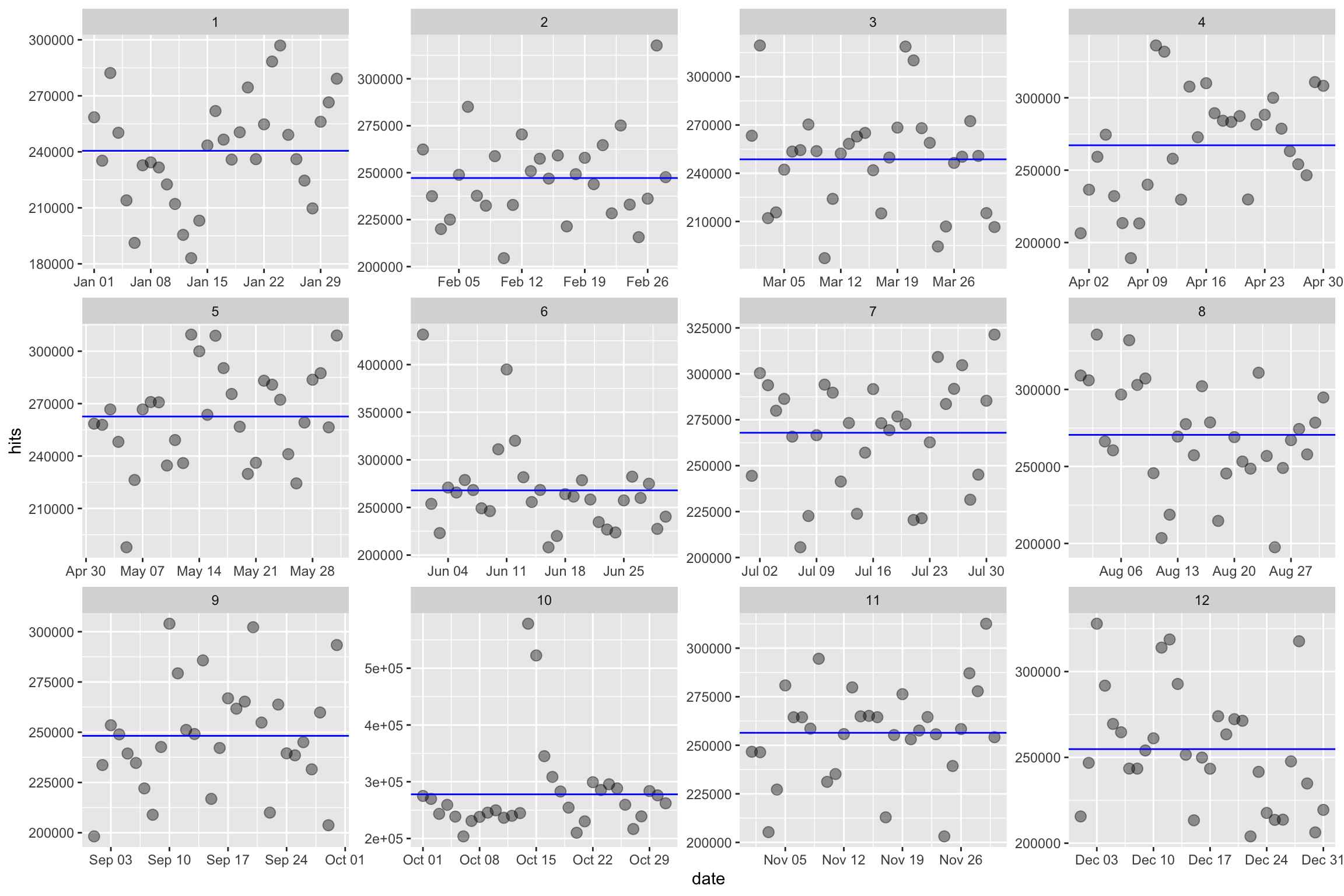
Que se passe-t-il si nous ajoutons un repère à 3 écarts-type de notre moyenne mensuelle.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
mutate(mean.month = mean(hits), med.month = median(hits)) %>%
mutate(sd = sd(hits), Usd = (mean.month + 3 * sd), Lsd = (mean.month - 3 * sd)) %>%
ungroup() %>%
ggplot() +
aes(date, hits, col = (hits > Usd | hits < Lsd)) +
geom_point(size = 2, alpha = .75) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
geom_hline(aes(yintercept = Lsd), col = "red") +
geom_hline(aes(yintercept = Usd), col = "red") +
theme(legend.position = "none") +
facet_wrap(~month, scales = "free")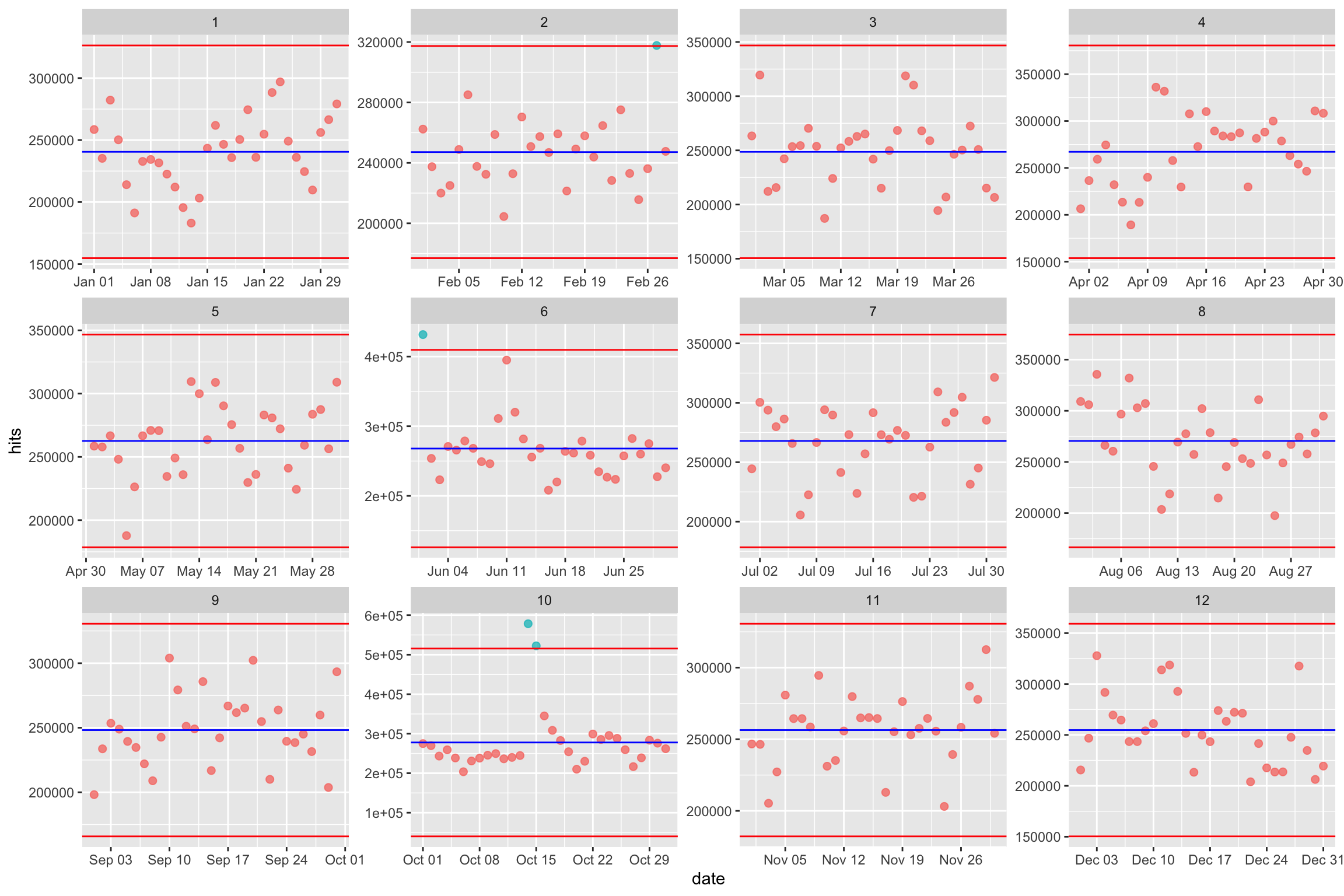
On voit que les valeurs max sont exclues de l’intervalle -3*sd, +3*sd, ne concerne plus que 4 valeurs :
- février
- juin
- octobre
Voyons ce que la méthode donne pour 2017. Fixons l’échelle des ordonnées.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2017-01-01", date < "2018-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
mutate(mean.month = mean(hits), med.month = median(hits)) %>%
mutate(sd = sd(hits), upper.sd = (mean.month + 3 * sd), lower.sd = (mean.month - 3 * sd)) %>%
ungroup() %>%
ggplot() +
aes(date, hits, col = (hits > upper.sd)) +
geom_line(aes(group = month), col = "black") +
geom_point(size = 2, alpha = .75) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
geom_hline(aes(yintercept = lower.sd), col = "red") +
geom_hline(aes(yintercept = upper.sd), col = "red") +
theme(legend.position = "none") +
labs(title = "2017") +
facet_wrap(~month, scale = "free_x")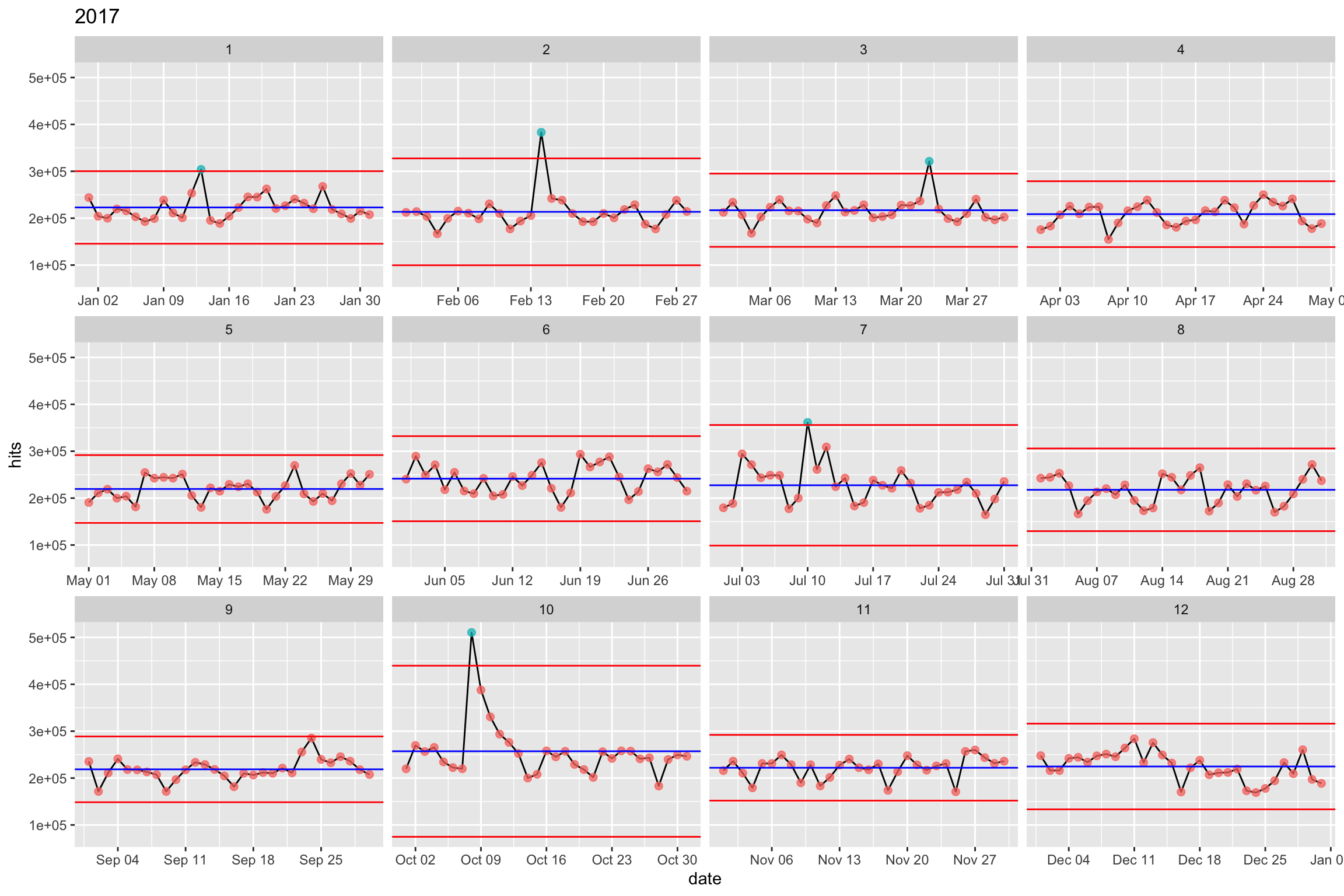
5 jours spécifiques pour 2017. C’est déjà mieux que 12
approche 3 : BoxPlot
Et si finalement, l’identification pouvait se faire grâce aux boites à moustache ? En effet les valeurs aberrantes sont facilement visualisables. Pour rappel, nous étions sur une identification en février, juin et octobre.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
ggplot() +
aes(factor(month), hits) +
geom_boxplot(outlier.colour = "red", outlier.size = 5) +
geom_jitter(width = 0.05, size = 5, col = "blue", alpha = 0.3) +
theme(legend.position = "none") +
labs(title = "2018")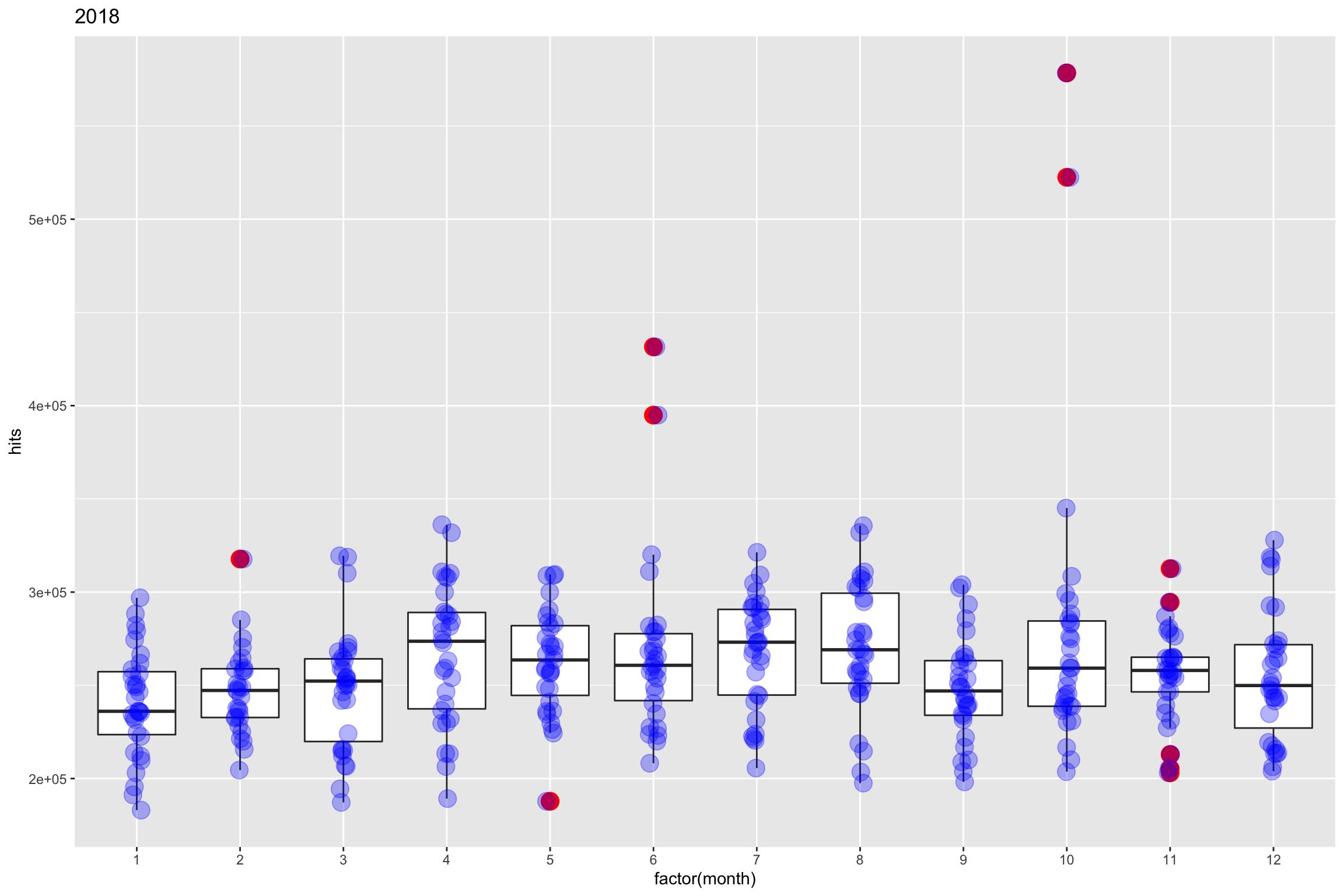
Nous voyons effectivement qu’il est possible d’identifier les valeurs aberrantes grâce à ce type de graphique. Comment ces valeurs sont calculées? Simplement avec l’IQR, soit l’Inter-Quartile-Range. IQR = Q3 - Q1
- Q1 - 1.5*IQR
- Q3 + 1.5*IQR
La fonction boxplot.stat permet d’identifier les valeurs anormales.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
select(month, hits) %>%
nest() %>%
mutate(outliers = map(data, ~ boxplot.stats(pull(.x)))) %>%
pull(outliers) %>% # output is a list
map("out") %>% # keep only the "out" element
set_names(paste0("month_", 12:01)) %>% #set month name
compact() %>% # discard month with NULL
enframe() %>% # transform list a nested list
unnest(cols = c(value))## # A tibble: 11 x 2
## name value
## <chr> <dbl>
## 1 month_11 312577
## 2 month_11 203102
## 3 month_11 212915
## 4 month_11 294541
## 5 month_11 205289
## 6 month_10 522478
## 7 month_10 578463
## 8 month_6 394929
## 9 month_6 431512
## 10 month_5 187793
## 11 month_2 317729Approche 4 : tsoutliers du package forecast
Le package forecast propose la fonction tsoutliers pour identifier des outliers et retourner la position (index). La fonction propose aussi une valeur de remplacement. Petit détail, il faut en input une TimeSerie. Testons cela sur 2017 et 2018.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2017-01-01", date < "2019-01-01") %>%
select(date, hits) %>%
arrange(date) %>%
select(hits) %>%
ts() %>%
forecast::tsoutliers()## $index
## [1] 45 191 281 282 517 527 652 653
##
## $replacements
## [1] 223845.0 230671.5 256749.3 293607.7 281399.0 315575.0 278185.7 311630.3Les index retournés sont utilisés pour sélectionner les dates.
cim %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2017-01-01", date < "2019-01-01") %>%
select(date, hits) %>%
arrange(date) %>%
slice(c(45, 191, 281, 282, 517, 527, 652, 653))## # A tibble: 8 x 2
## date hits
## <date> <dbl>
## 1 2017-02-14 383061
## 2 2017-07-10 361443
## 3 2017-10-08 510494
## 4 2017-10-09 387819
## 5 2018-06-01 431512
## 6 2018-06-11 394929
## 7 2018-10-14 578463
## 8 2018-10-15 522478Ce qui est intéressant ici c’est que les valeurs sont identifiées sur les 2 années sans groupement par mois. Les dates retournées sont les mêmes que celles identifiées dans l’approche 2.
Approche 5 : Control Chart
Moving Range
Cette méthode est inspirée de ce post post. Elle se repose sur le Moving Range, il s’agit de calculer la différence absolue entre chaque suite de valeurs (en quelque sorte les valeurs lagguées) divisée par une constante. Nous reviendrons sur cette constante un peu plus loin. Commençons par définir une nouvelle table.
En réalité il s’agit d’un control chart ou carte de qualité. Une carte de contrôle, ou plus exactement un graphique de contrôle sont des outils utilisés dans le domaine du contrôle de la qualité afin de maîtriser un processus. Elle permet de déterminer le moment où apparaît une cause particulière de variation d’une caractéristique, entraînant une altération du processus. Par exemple un processus de fabrication pourra être mis à l’arrêt avant de produire des pièces qui seront non conformes. (source : wikipedia)
La raison d’utiliser une plage c’est que cela permet de ne pas prendre l’écart-type (standard déviation - qui calcule la variation sur l’ensemble des valeurs) et donc de permettre l’identification de variations aléatoires non systématiques.
cim2 <- cim %>%
arrange(date) %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
group_by(month) %>%
mutate(mean.month = mean(hits), med.month = median(hits)) %>%
mutate(sd = sd(hits), upper.sd = (mean.month + 3 * sd), lower.sd = (mean.month - 3 * sd)) %>%
ungroup()Calculons la différence entre 2 dates journalières.
cim2 %>%
mutate(diff = hits - lag(hits)) %>%
select(date, month, hits, diff) %>%
ggplot() +
aes(date, diff) +
geom_col() +
labs(title = "2018") +
facet_wrap(~month, scale = "free_x")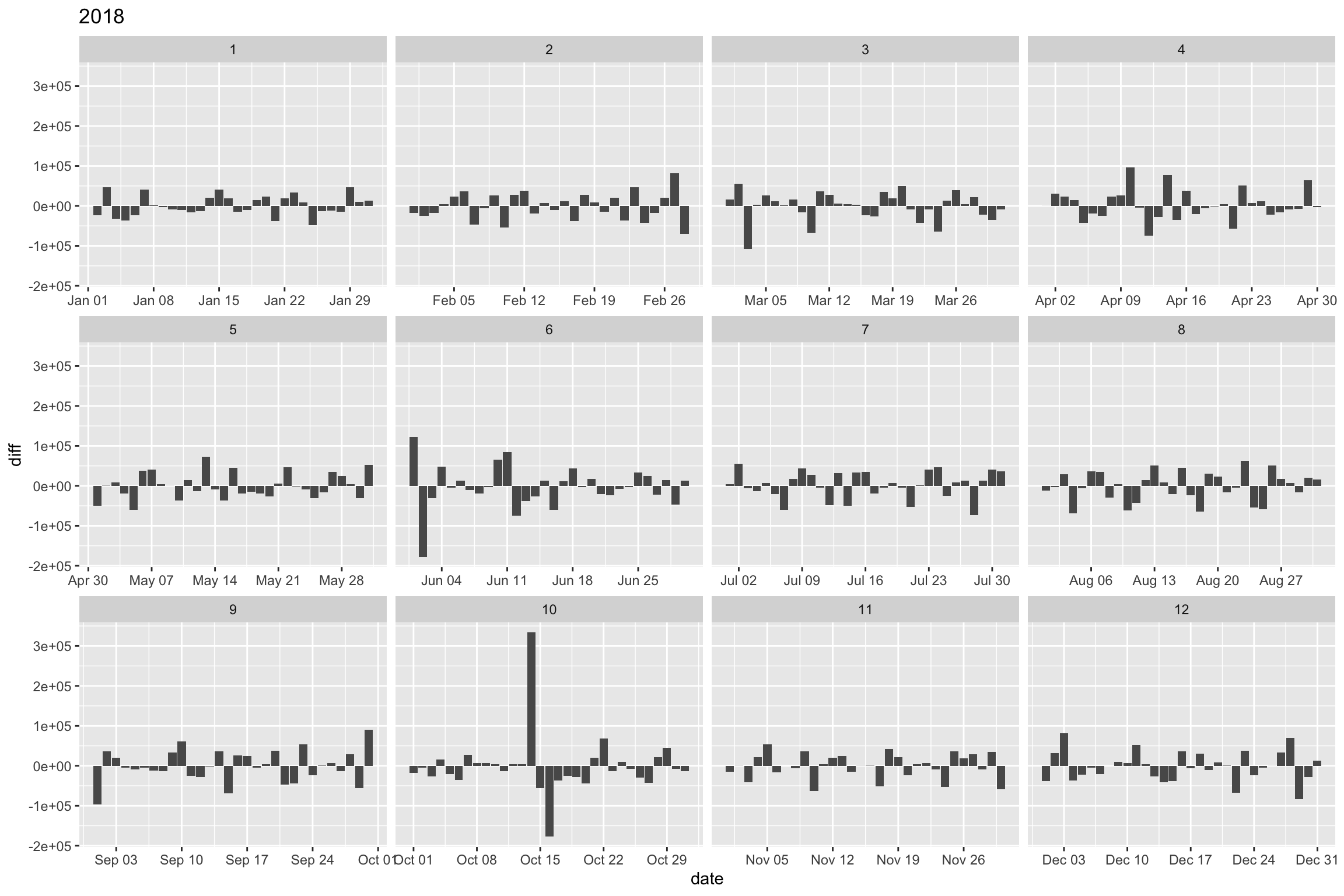
Transformons les valeurs en valeurs absolues :
cim2 %>%
mutate(diff = abs(hits - lag(hits))) %>%
select(date, month, diff) %>%
ggplot() +
aes(date, diff) +
geom_col() +
labs(title = "2018") +
facet_wrap(~month, scale = "free_x")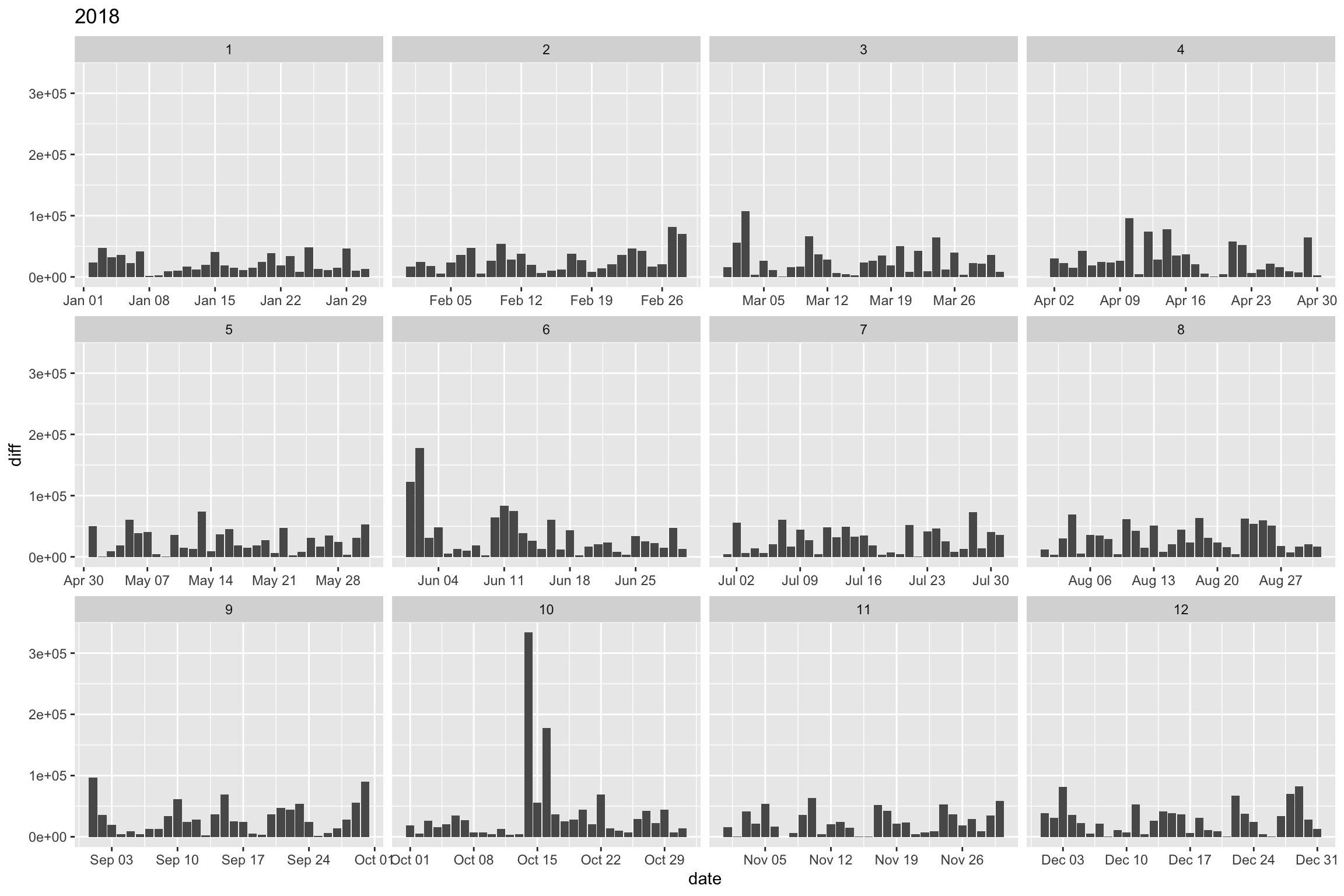
Calculons la moyenne de ces différences : mean(mR)
cim2 %>%
mutate(diff = abs(hits - lag(hits))) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
select(date, month, diff, mean_mr) %>%
pull(mean_mr) %>%
unique()## [1] 28633.46Et appliquons la division par la constante 1.128 pour N = 2.
Soit seq_dv = mean_mr / (constante = 1.128)
cim2 %>%
mutate(diff = abs(hits - lag(hits))) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
mutate(seq_dev = mean_mr/1.128) %>% #seq_dev calculation
select(date, month, diff, seq_dev) %>%
pull(seq_dev) %>%
unique()## [1] 25384.27Constante d2(), d3()…
Kenith Grey, le développeur du package ggQC explique bien comment calculer les constantes utilisées avec les control charts.
Vous pouvez consulter son article ici.
Lower et Upper Control Limit
Comme lors du calcul de l’intervalle de confiance d’une moyenne, nous appliquons cette valeur à la moyenne des sessions. Soit mean + 3 * seq_dev, mean - 3 * seq_dev.
cim2.control <- cim2 %>%
mutate(diff = abs(hits - lag(hits))) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
mutate(seq_dev = mean_mr/1.128) %>%
mutate(lower.cl = mean.month - 3 * seq_dev, upper.cl = mean.month + 3 * seq_dev) %>%
select(date, month, hits, mean.month, lower.sd, upper.sd, lower.cl, upper.cl)
cim2.control %>% head()## # A tibble: 6 x 8
## date month hits mean.month lower.sd upper.sd lower.cl upper.cl
## <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2018-01-01 1 258510 240528. 154745. 326311. 164375. 316681.
## 2 2018-01-02 1 235248 240528. 154745. 326311. 164375. 316681.
## 3 2018-01-03 1 282221 240528. 154745. 326311. 164375. 316681.
## 4 2018-01-04 1 250210 240528. 154745. 326311. 164375. 316681.
## 5 2018-01-05 1 213997 240528. 154745. 326311. 164375. 316681.
## 6 2018-01-06 1 191218 240528. 154745. 326311. 164375. 316681.cim2.control %>%
ggplot() +
aes(date, hits, col = (hits > upper.cl | hits < lower.cl)) +
geom_line(aes(group = month), col = "black") +
geom_point(size = 2, alpha = .75) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
geom_hline(aes(yintercept = lower.cl), col = "red") +
geom_hline(aes(yintercept = upper.cl), col = "red") +
labs(title = "2018") +
facet_wrap(~month, scale = "free_x") +
theme(legend.position = "none")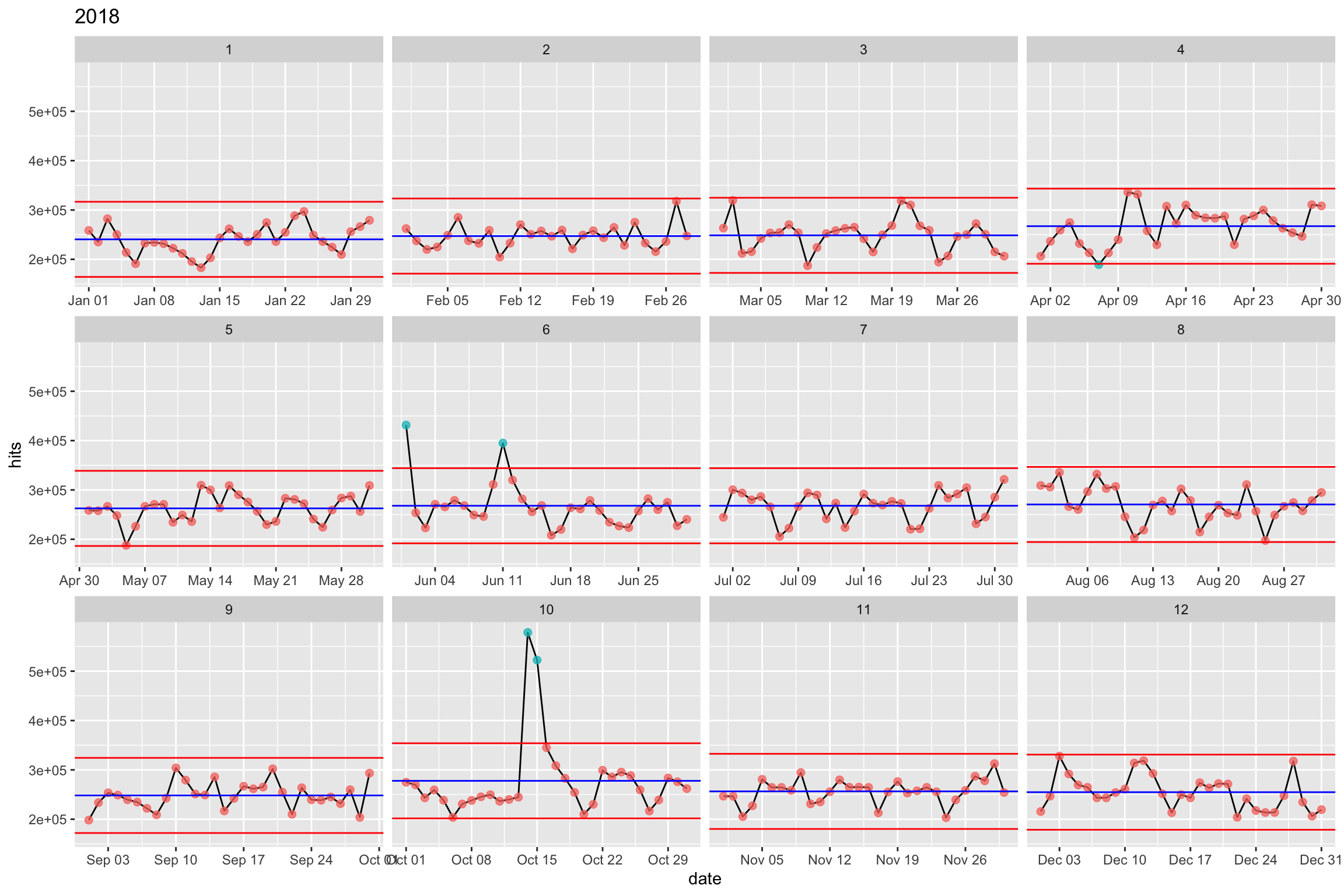
Comparons avec la méthode de la déviation standard.
cim2.control %>%
ggplot() +
aes(date, hits, col = (hits > upper.sd | hits < lower.sd)) +
geom_line(aes(group = month), col = "black") +
geom_point(size = 2, alpha = .75) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
geom_hline(aes(yintercept = lower.cl), col = "red") +
geom_hline(aes(yintercept = upper.cl), col = "red") +
geom_hline(aes(yintercept = upper.sd), col = "purple") +
geom_hline(aes(yintercept = lower.sd), col = "purple") +
labs(title = "2018") +
theme(legend.position = "none") +
facet_wrap(~month, scale = "free_x")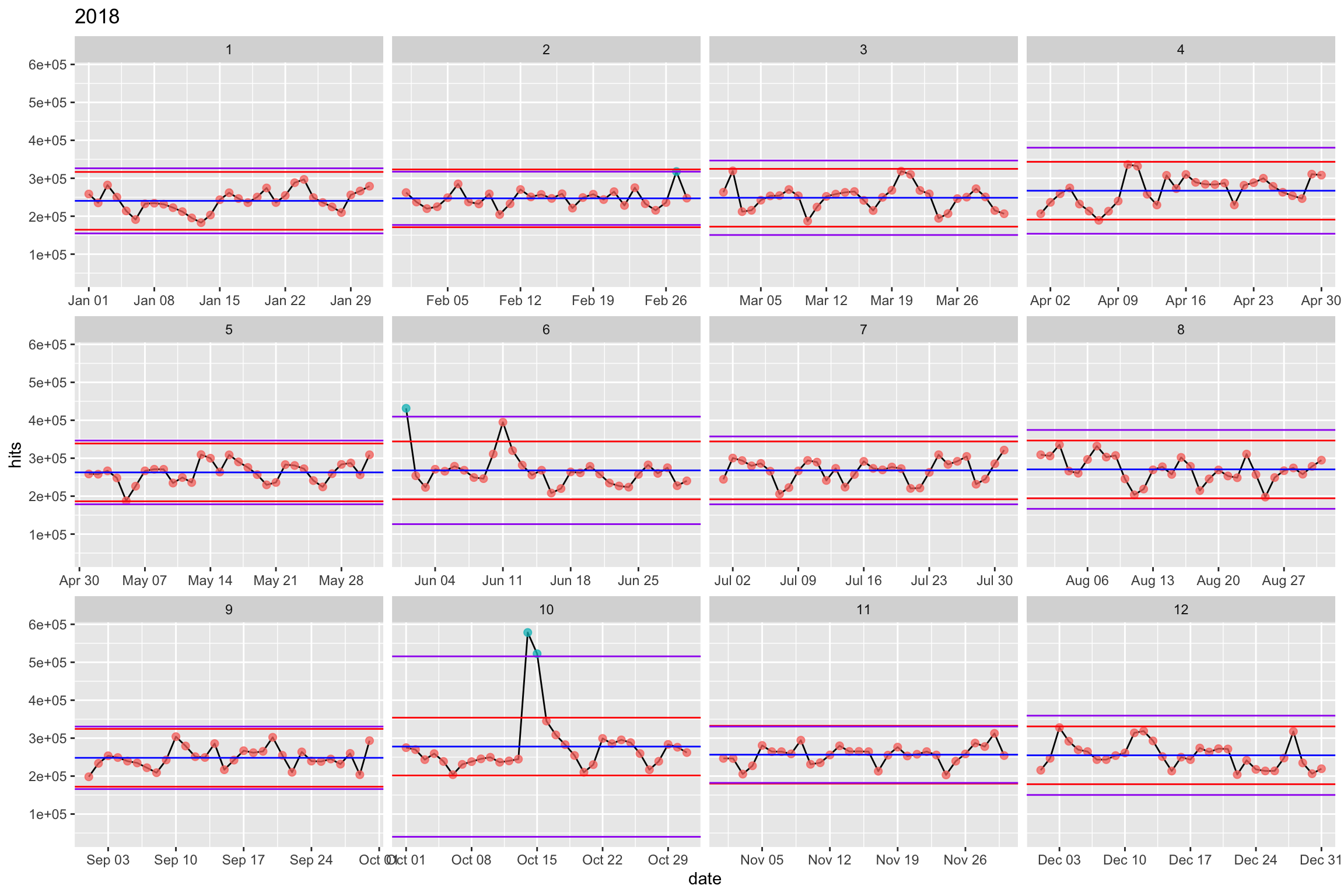
On voit effectivement que la zone déterminée par la deviation standard est moins robuste aux outliers. Et sur 2017? Adaptons le graphique afin d’y afficher les dates.
cim %>%
arrange(date) %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
mutate(year = lubridate::year(date)) %>%
mutate(diff = abs(hits - lag(hits))) %>%
group_by(year, month) %>%
mutate(mean.month = mean(hits)) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
mutate(seq_dev = mean_mr/1.128) %>%
mutate(lower.cl = mean.month - 3 * seq_dev, upper.cl = mean.month + 3 * seq_dev) %>%
select(date, year, month, hits, mean.month, lower.cl, upper.cl) %>%
ggplot() +
aes(date, hits, col = (hits > upper.cl | hits < lower.cl)) +
geom_line(aes(group = month), col = "black") +
geom_point(size = 4, alpha = 1) +
geom_hline(aes(yintercept = mean.month), col = "blue") +
scale_x_date(breaks = "day", date_labels = "%a", minor_breaks = NULL) +
geom_hline(aes(yintercept = lower.cl), col = "red") +
geom_hline(aes(yintercept = upper.cl), col = "red") +
geom_text(aes(x = date, y = hits, label = format(date, "%d")), col = "black", size = 2) +
theme(legend.position = "none", axis.text.x = element_text(size = 6, angle = 90)) +
facet_wrap(year ~month, scales = "free_x") 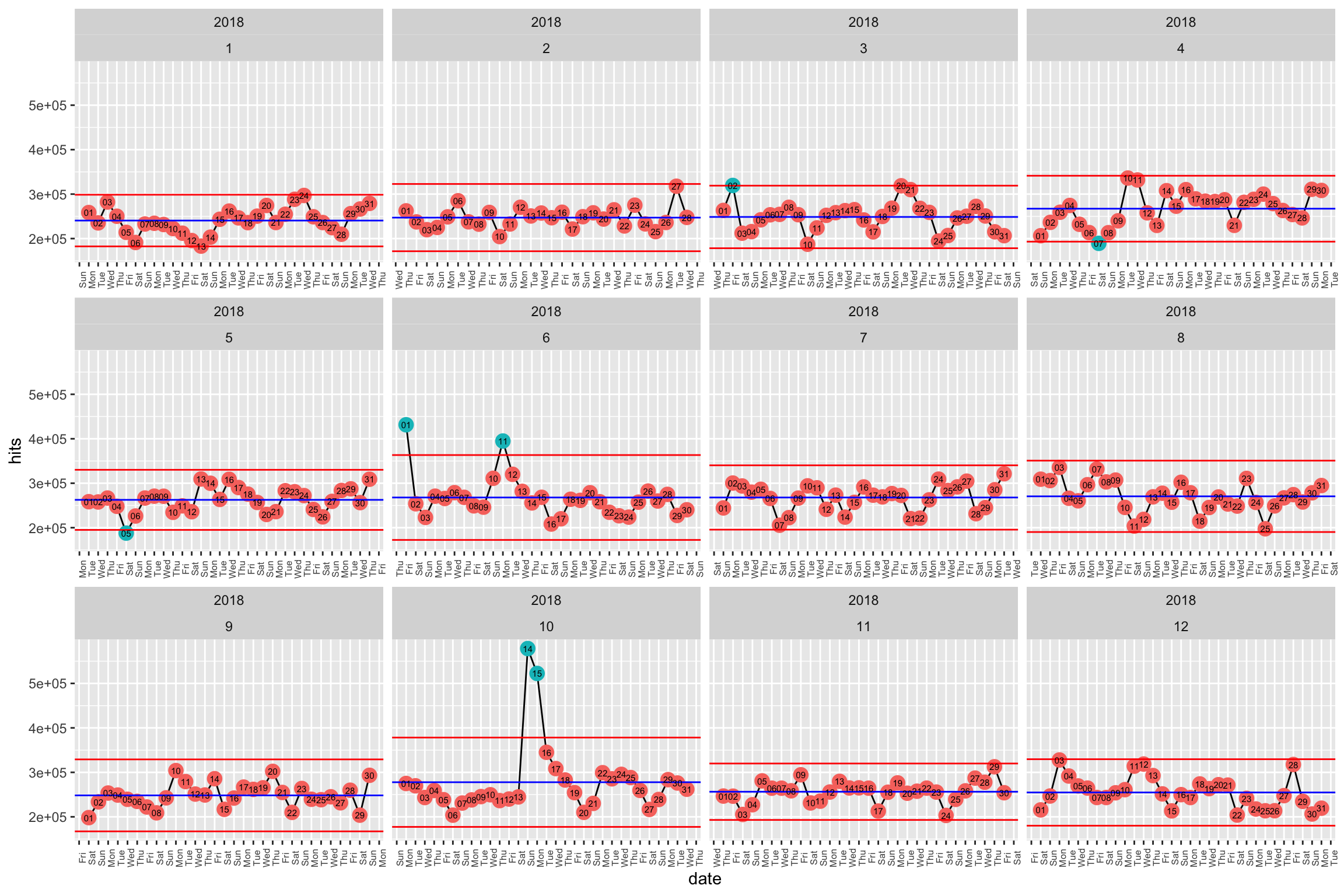
Sortons les dates anormales :
cim %>%
arrange(date) %>%
filter(metrics == "sessions") %>%
filter(site %in% c("RTL Luxembourg")) %>%
filter(date >= "2018-01-01", date < "2019-01-01") %>%
mutate(month = lubridate::month(date)) %>%
mutate(year = lubridate::year(date)) %>%
mutate(diff = abs(hits - lag(hits))) %>%
group_by(year, month) %>%
mutate(mean.month = mean(hits)) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
mutate(seq_dev = mean_mr/1.128) %>%
mutate(lower.cl = mean.month - 3 * seq_dev, upper.cl = mean.month + 3 * seq_dev) %>%
select(site, date, year, month, hits, mean.month, lower.cl, upper.cl)%>%
filter(hits >= upper.cl | hits <= lower.cl) %>%
pull(date)## [1] "2018-03-02" "2018-04-07" "2018-05-05" "2018-06-01" "2018-06-11"
## [6] "2018-10-14" "2018-10-15"via le package qicharts2
Le package qicharts permet de réaliser différents types de control chart. Run chart, I chart…
qicharts2::qic(x = date, y = hits, data = cim2.control)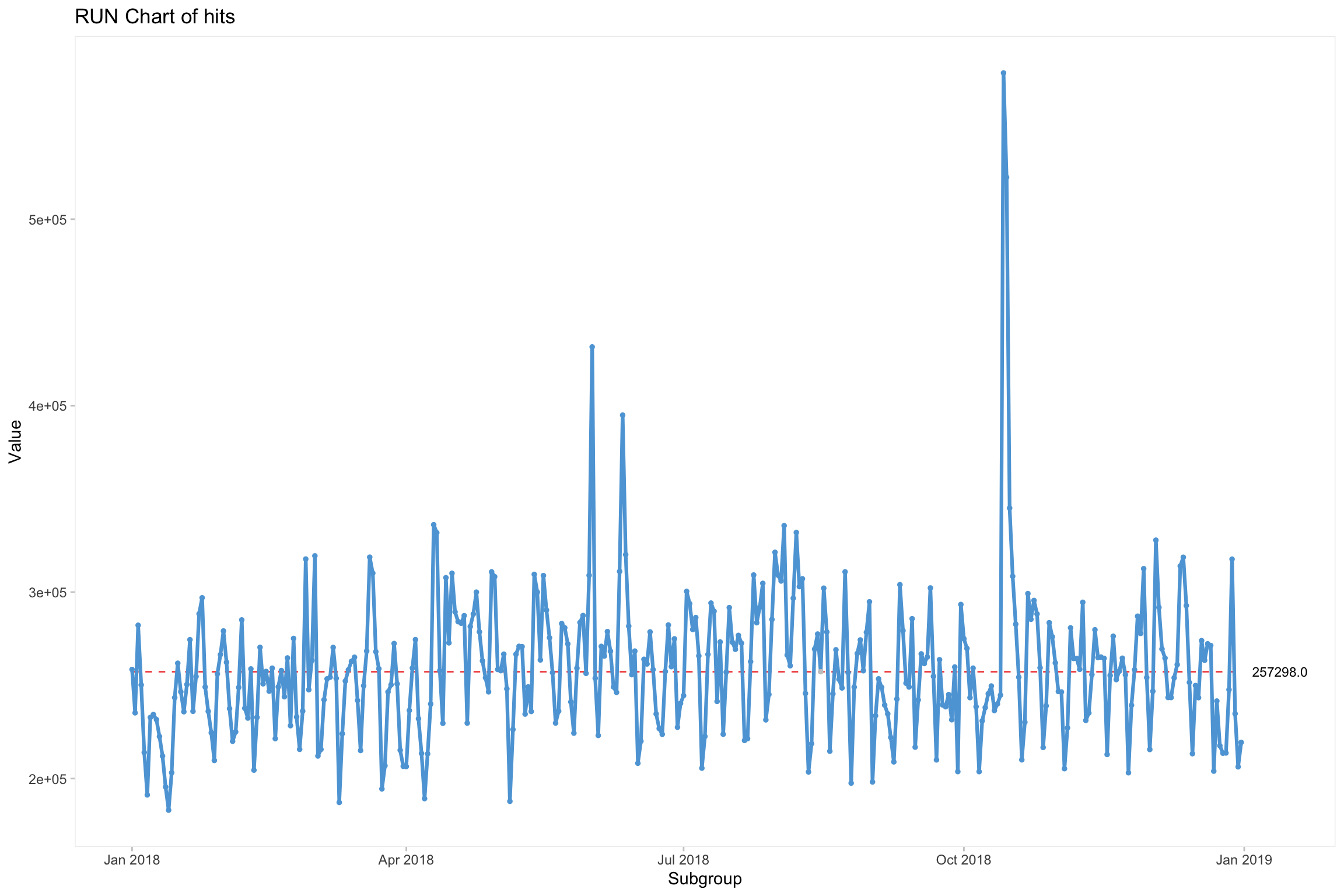
qicharts2::qic(x = date, y = hits, chart = "i", data = cim2.control)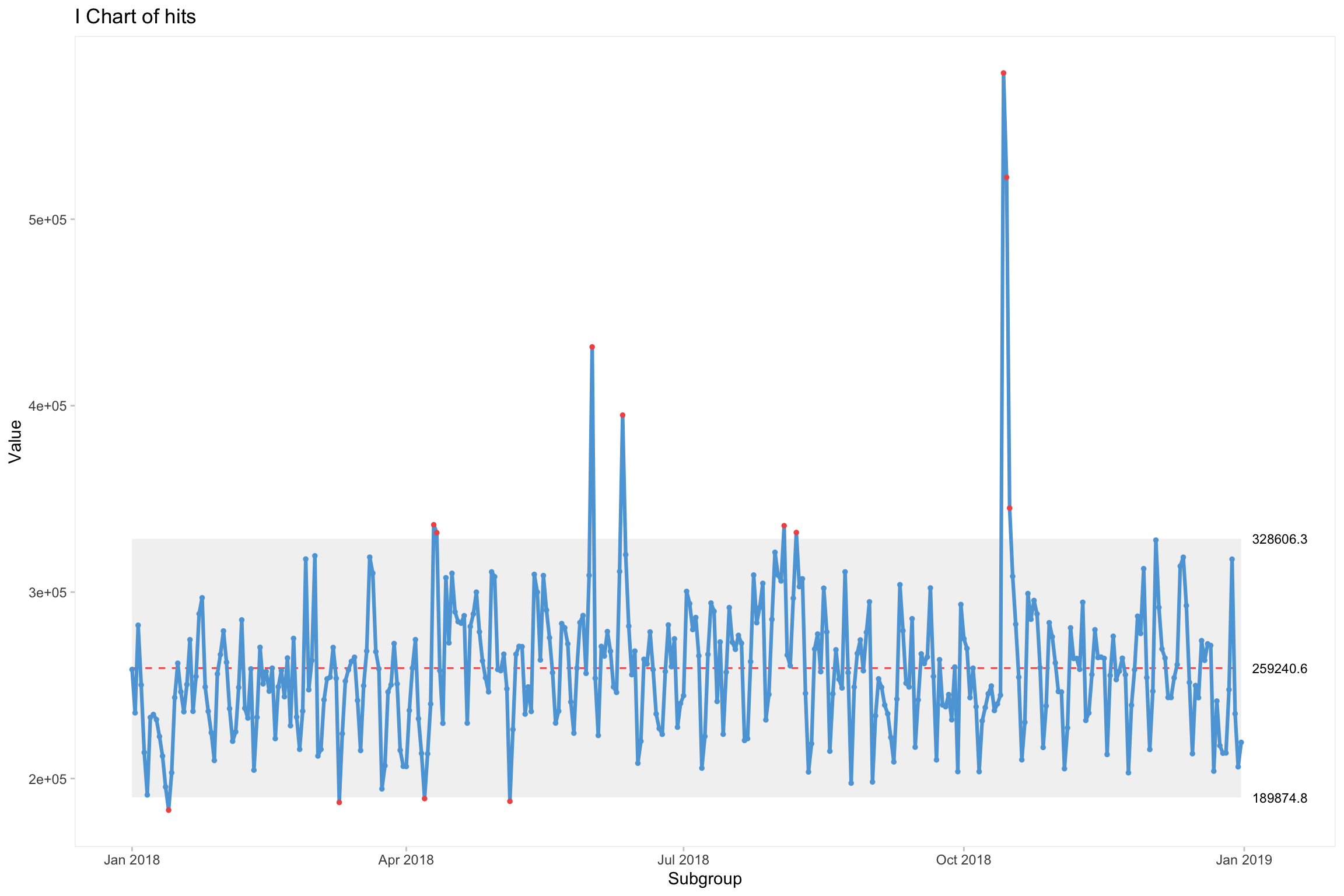
Aller plus loin : Une fonction spécifique pour le CIM
Nous voici à la fin de cette exploration. Pour allez un peu plus loin, nous allons écrire une fonction simplifiant l’identification des jours dont les mesures de sessions dans ce cas sont aberrantes.
Nous avons notre série temporelle en entrée et en sortie les dates supérieures à upper.cl ou inférieures à lower.cl. Nous y incluons aussi la génération d’un graphique pour visualiser les dates de la série.
detect_date <- function(df, metric, website, min.date, max.date, graph = TRUE, lcl = TRUE, list = TRUE) {
options(scipen = 999)
# Calculte upper and lower control limit
df %>%
arrange(date) %>%
filter(metrics == metric) %>%
filter(site %in% website) %>%
filter(date >= min.date, date < max.date) %>%
mutate(month = lubridate::month(date)) %>%
mutate(year = lubridate::year(date)) %>%
group_by(site, year, month) %>%
mutate(diff = abs(hits - lag(hits))) %>%
mutate(mean.month = mean(hits)) %>%
mutate(mean_mr = mean(diff, na.rm = TRUE)) %>%
mutate(seq_dev = mean_mr/1.128) %>%
mutate(lower.cl = mean.month - 3 * seq_dev, upper.cl = mean.month + 3 * seq_dev) %>%
select(site, date, year, month, hits, mean.month, lower.cl, upper.cl) %>%
group_by(site) %>%
nest() -> df.control
# Function to generate plot
draw_chart <- as_mapper(~ ggplot(.x) +
aes(date, hits, col = !(hits > upper.cl | hits < lower.cl)) +
geom_line(aes(group = month), col = "black") +
geom_hline(aes(yintercept = mean.month), col = "blue") +
scale_x_date(breaks = "day", date_labels = "%a", minor_breaks = NULL) +
geom_hline(aes(yintercept = lower.cl), col = "red") +
geom_hline(aes(yintercept = upper.cl), col = "red") +
geom_point(size = 4, alpha = 1) +
geom_text(aes(x = date, y = hits, label = format(date, "%d")), , col = "black", size = 2) +
ggthemes::theme_solarized_2() +
theme(legend.position = "none",
axis.text.x = element_text(size = 6, angle = 90),
axis.title = element_blank(),
plot.margin = unit(c(1.5, 1.5, 1.5, 1.5), "cm")) +
labs(title = .y) +
facet_wrap(year ~month, scales = "free_x")
)
df.control %>%
mutate(plot = map2(data, site, draw_chart)) -> df.control_graph
# Recode Site name in CDN
df.control %>%
unnest(cols = c(data)) %>%
ungroup() %>%
mutate(site = case_when(
site == "RTL Luxembourg" ~ "rtl.lu",
site == "L'essentiel" ~ "lessentiel.lu",
site == "Wort.lu" ~ "wort.lu",
site == "Tageblatt" ~ "tageblatt.lu",
site == "Revue" ~ "revue.lu",
site == "PaperJam" ~ "paperjam.lu",
site == "Luxweb.com" ~ "luxweb.com",
site == "Le Jeudi" ~ "jeudi.lu",
site == "IMMOTOP.LU" ~ "immotop.lu",
site == "Editus" ~ "editus.lu",
site == "atOffice.lu" ~ "atoffice.lu",
site == "Luxtimes.lu" ~ "luxtimes.lu",
site == "Le Quotidien" ~ "quotidien.lu",
site == "Eldoradio" ~ "eldoradio.lu",
site == "Delano" ~ "delano.lu",
site == "Luxauto" ~ "luxauto.lu",
site == "Wortimmo.lu" ~ "wortimmo.lu" ,
site == "Explorator" ~ "explorator.lu",
site == "atHome.lu" ~ "athome.lu")) -> df.control.recoded
# Filter output from argument set in the function
if(lcl) {
df.control.recoded %>%
filter(hits >= upper.cl | hits <= lower.cl) %>%
select(site, date) -> df.control_date
} else {
df.control.recoded %>%
filter(hits >= upper.cl) %>%
select(site, date) -> df.control_date
}
# Transfom in list if set as argument
if(list) {
df.control_date %>%
plyr::dlply(.variables = "site") %>%
map(2) -> df.control_date
}
# Show graph if set as argument
if(graph) {
list(df.control_graph$plot, df.control_date) %>%
flatten()
} else {
df.control_date
}
}Testons la fonction.
detect_date(cim,
metric = "sessions",
website = c("RTL Luxembourg", "L'essentiel", "Wort.lu"),
min.date = "2018-01-01",
max.date = "2019-01-01",
graph = FALSE,
lcl = FALSE,
list = FALSE)## # A tibble: 16 x 2
## site date
## <chr> <date>
## 1 rtl.lu 2018-06-01
## 2 rtl.lu 2018-06-11
## 3 rtl.lu 2018-10-14
## 4 rtl.lu 2018-10-15
## 5 wort.lu 2018-01-31
## 6 wort.lu 2018-03-20
## 7 wort.lu 2018-05-16
## 8 wort.lu 2018-06-01
## 9 wort.lu 2018-10-14
## 10 wort.lu 2018-10-15
## 11 wort.lu 2018-10-16
## 12 lessentiel.lu 2018-06-11
## 13 lessentiel.lu 2018-06-19
## 14 lessentiel.lu 2018-07-31
## 15 lessentiel.lu 2018-10-01
## 16 lessentiel.lu 2018-12-12En sortie nous avons bien une liste avec des dates pour chaque site et le graphique approprié.
Encore plus loin : 2 fonctions pour composer une url de recherche.
Nous allons générer dans une table les URL afin de consulter l’actualité pour chaque date en sortie sur Google. Pour cela, nous allons créer 2 fonctions d’encodage.
# Creating encoder with as_mapper
encode_date <- as_mapper(~ .x %>%
as.Date() %>%
format("%m/%d/%Y") %>%
str_replace_all("/", "%2F")
)
encode_url <- function(x, y) {
paste0("https://www.google.lu/search?q=", y, "&tbs=cdr%3A1%2C", "cd_min%3A",
encode_date(x), "%2Ccd_max%3A", encode_date(x), "&tbm=nws")
} Astuce avec enframe() du package tibble
J’ai rencontré ce problème : transformer une liste en table dont chaque élément est de longueur différente.
as_tibble fonctionne si la longueur de chaque élément est identique.
Par ex. cela fonctionne ici :
list(site1 = c("url1", "url2"), site2 = c("url2", "url3")) %>%
as_tibble()## # A tibble: 2 x 2
## site1 site2
## <chr> <chr>
## 1 url1 url2
## 2 url2 url3Mais pas ici :
list(site1 = c("url1", "url2"), site2 = c("url2", "url3", "url3")) %>%
as_tibble()La solution est de passé par enframe() du package tibble, puis unnest() pour avoir une table complète.
list(site1 = c("url1", "url2"), site2 = c("url2", "url3", "url3")) %>%
enframe() %>%
unnest(cols = c(value))## # A tibble: 5 x 2
## name value
## <chr> <chr>
## 1 site1 url1
## 2 site1 url2
## 3 site2 url2
## 4 site2 url3
## 5 site2 url3Composons une fonction spécifique list_to_df:
list_to_df <- compose(unnest, enframe)
list(site1 = c("url1", "url2"), site2 = c("url2", "url3", "url3")) %>% list_to_df()## # A tibble: 5 x 2
## name value
## <chr> <chr>
## 1 site1 url1
## 2 site1 url2
## 3 site2 url2
## 4 site2 url3
## 5 site2 url3Table des dates avec URL et occurrences.
Nous arrivons à la fin de notre article Nous allons générer une table HTML avec kabble et kabbleExtra comprenant les dates, répétition et URL vers Google en lien.
detect_date(cim,
metric = "sessions",
website = c("RTL Luxembourg", "L'essentiel", "Wort.lu"),
min.date = "2017-01-01",
max.date = "2019-01-01",
graph = FALSE,
lcl = FALSE,
list = FALSE) %>%
mutate(url = encode_url(date, site)) %>%
group_by(date) %>%
mutate(occurency = n()) %>%
arrange(date, occurency, site) %>%
select(date, occurency, site, url) %>%
mutate(url = kableExtra::text_spec("link", link = url)) %>%
knitr::kable("html", escape = FALSE) %>%
kableExtra::kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) | date | occurency | site | url |
|---|---|---|---|
| 2017-01-13 | 1 | rtl.lu | link |
| 2017-01-19 | 1 | lessentiel.lu | link |
| 2017-02-14 | 3 | lessentiel.lu | link |
| 2017-02-14 | 3 | rtl.lu | link |
| 2017-02-14 | 3 | wort.lu | link |
| 2017-03-23 | 3 | lessentiel.lu | link |
| 2017-03-23 | 3 | rtl.lu | link |
| 2017-03-23 | 3 | wort.lu | link |
| 2017-07-10 | 1 | rtl.lu | link |
| 2017-09-04 | 1 | wort.lu | link |
| 2017-09-24 | 1 | rtl.lu | link |
| 2017-10-06 | 1 | lessentiel.lu | link |
| 2017-10-08 | 2 | rtl.lu | link |
| 2017-10-08 | 2 | wort.lu | link |
| 2017-10-09 | 2 | rtl.lu | link |
| 2017-10-09 | 2 | wort.lu | link |
| 2018-01-31 | 1 | wort.lu | link |
| 2018-03-20 | 1 | wort.lu | link |
| 2018-05-16 | 1 | wort.lu | link |
| 2018-06-01 | 2 | rtl.lu | link |
| 2018-06-01 | 2 | wort.lu | link |
| 2018-06-11 | 2 | lessentiel.lu | link |
| 2018-06-11 | 2 | rtl.lu | link |
| 2018-06-19 | 1 | lessentiel.lu | link |
| 2018-07-31 | 1 | lessentiel.lu | link |
| 2018-10-01 | 1 | lessentiel.lu | link |
| 2018-10-14 | 2 | rtl.lu | link |
| 2018-10-14 | 2 | wort.lu | link |
| 2018-10-15 | 2 | rtl.lu | link |
| 2018-10-15 | 2 | wort.lu | link |
| 2018-10-16 | 1 | wort.lu | link |
| 2018-12-12 | 1 | lessentiel.lu | link |