Partie 1. L’instrument

1. L’onde sonore

Sans rentrer dans trop de détail et en cherchant un peu sur le web, on apprend que le son est une onde produite par la vibration du support pouvant être solide, liquide ou gazeux. Dans le contexte qui nous intéresse, il s’agit de la vibration de l’air. En réalité ce sont les molécules qui vibrent à la suite de cette perturbation mécanique. Elles subissent de faibles variations de pression et s’entrechoquent pour transmettre la perturbation et ainsi subir de minuscules déplacements. Elles reviennent à leur position de départ une fois la perturbation passée.

Une onde sonore est souvent une onde mécanique longitudinale. En effet les molécules se déplacent parallèlement au sens de propagation de l’onde.

2. Quelques caractéristiques à savoir

Avant de créer une onde, nous allons définir quelques caractéristiques :

A. La période :

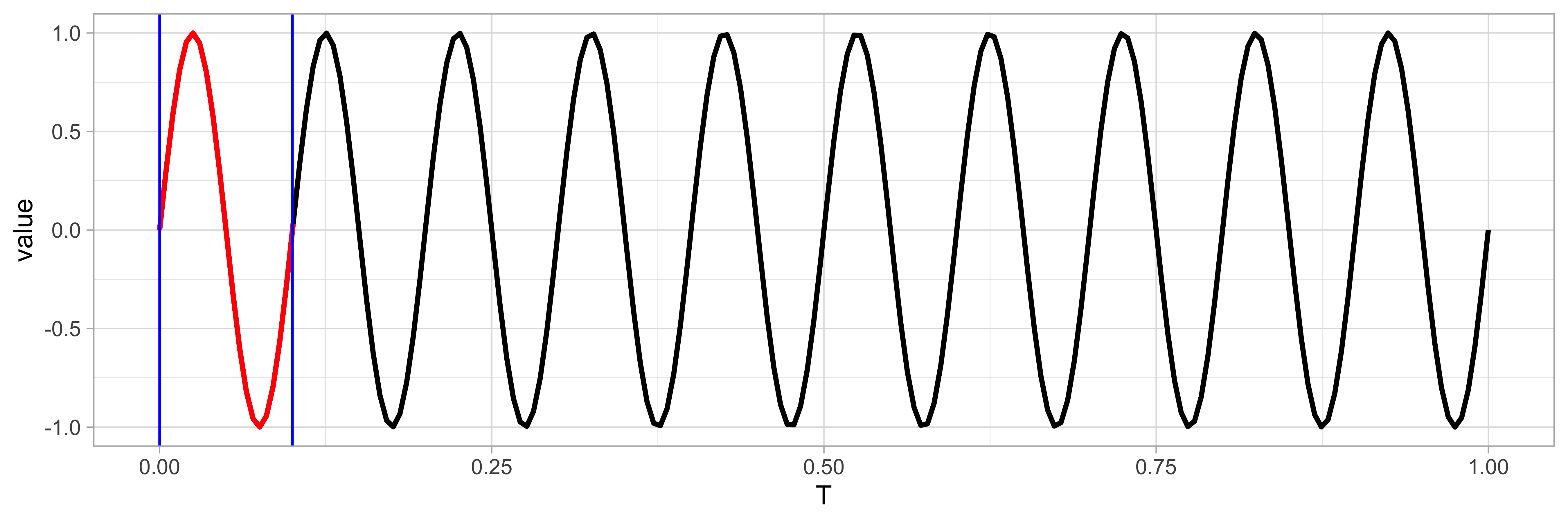
La période, notée T, est l’intervalle de temps séparant deux états vibratoires identiques et successifs. Nous voyons dans cet exemple une période de t = 0.1 indiquée par les 2 lignes verticales bleues. Nous utiliserons t pour un respect de syntaxe dans R.

B. La fréquence :

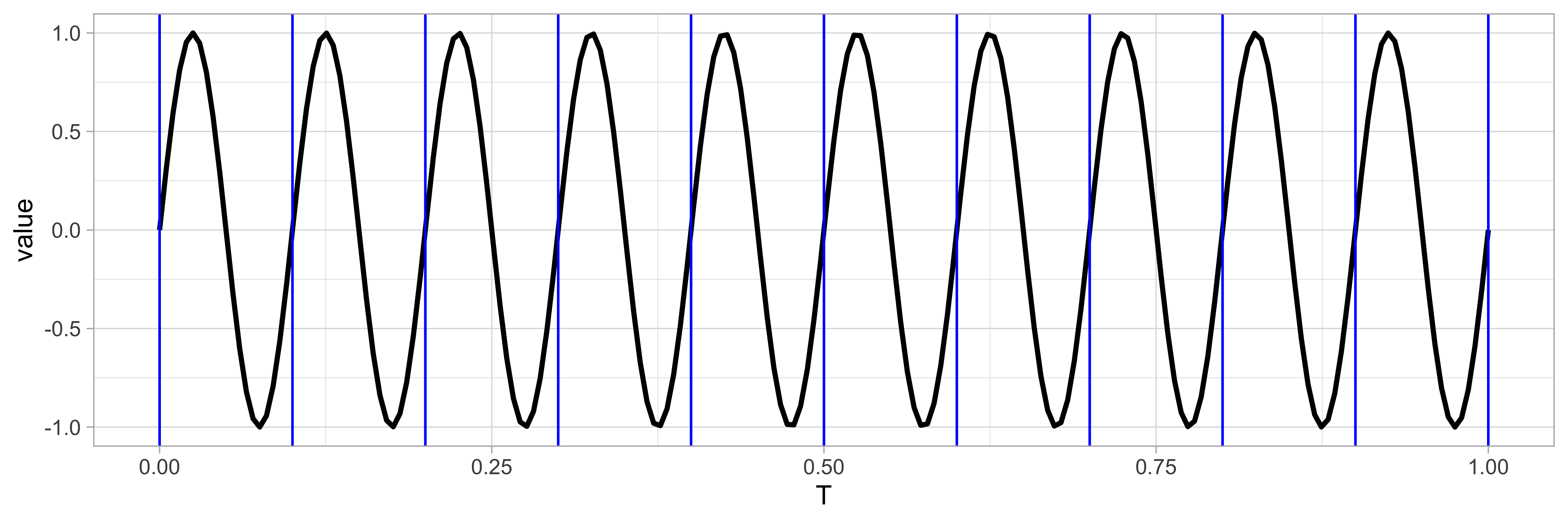
La fréquence est le nombre de périodes par unité de mesure. Cela correspond à l’inverse de la période :

\(\Large f = \frac{1}{T}\)

ou \(f\) est la fréquence en Hertz (Hz) et \(T\) la période en seconde (s). Dans l’exemple ci-dessous, la sinusoïde possède une période de 0,1 seconde. La fréquence correspond au nombre de périodes par seconde, c’est-à-dire le nombre de fois que le motif se répète, soit 10 fois. La fréquence est donc de 10 Hz. En appliquant l’inverse de la période on obtient également cette valeur : \(f = \frac{1}{0.1} = 10\) soit 10 Hz.

C. La durée :

Temps pendant lequel le milieu est perturbé. L’unité utilisée est la seconde (s) et sera enregistrée dans la variable d.

D. L’échantillonnage :

L’échantillonnage consiste à prélever les valeurs d’un signal à intervalles définis, généralement réguliers. Il produit une suite de valeurs discrètes nommées échantillons. Nous prendrons des échantillons de la fonction sinus sin.

Récapitulons. Nous définissons:

1. Une onde d’une durée de 1 sec;
2. Avec des périodes de 0.1 sec;
3. De fréquence f = (1 / 0.1);
4. Le nombre de prélévements, ici 100.

d <- 1
t <- 0.1
f <- (d / t)
s <- 100

3. Signal sinusoïdal

Selon Wikipedia, ce signal est une onde à une amplitude égale à la fonction sinusoïdale du temps. La fonction sinus permet de calculer le sinus d’un angle à partir de la valeur de cet angle.

Cela veut dire quoi concrètement ? Comment créer cette onde ? Pas question de cours de trigonométrie ici, rassurez-vous. Nous allons essayer d’interpréter l’animation issue de la page wikipedia pas à pas.

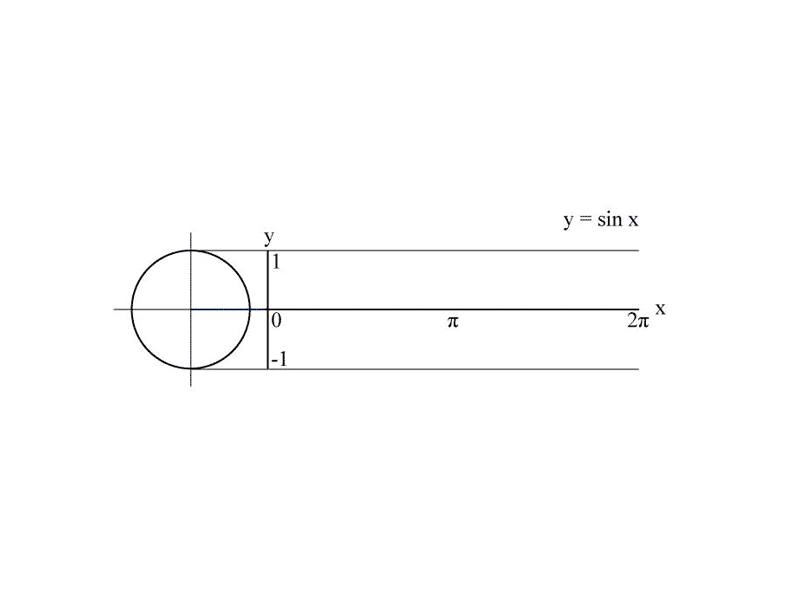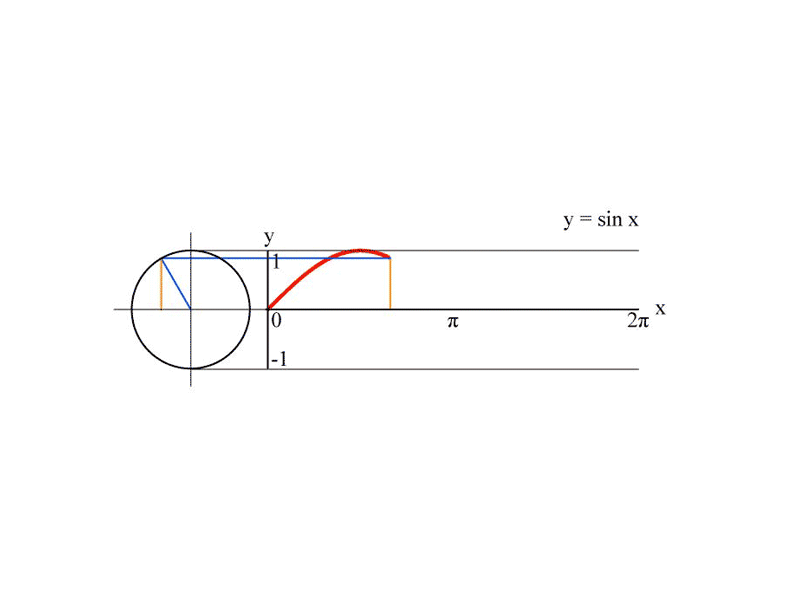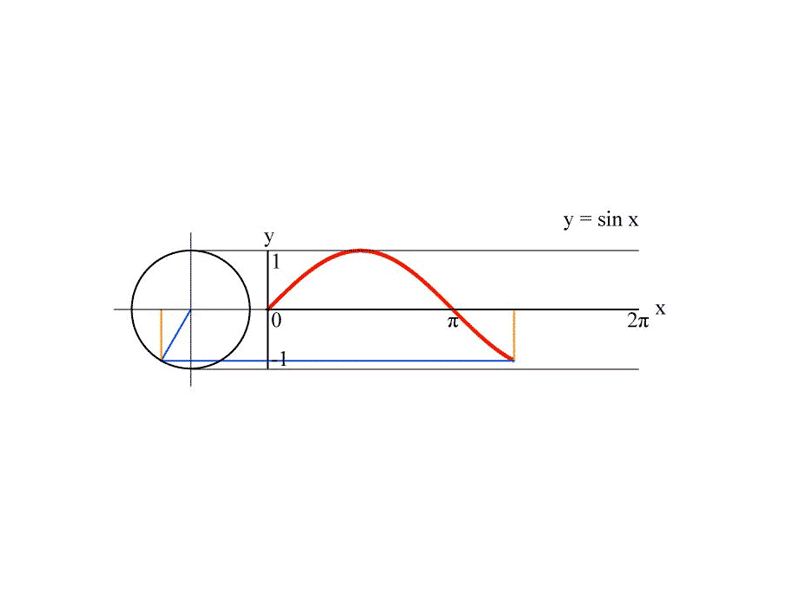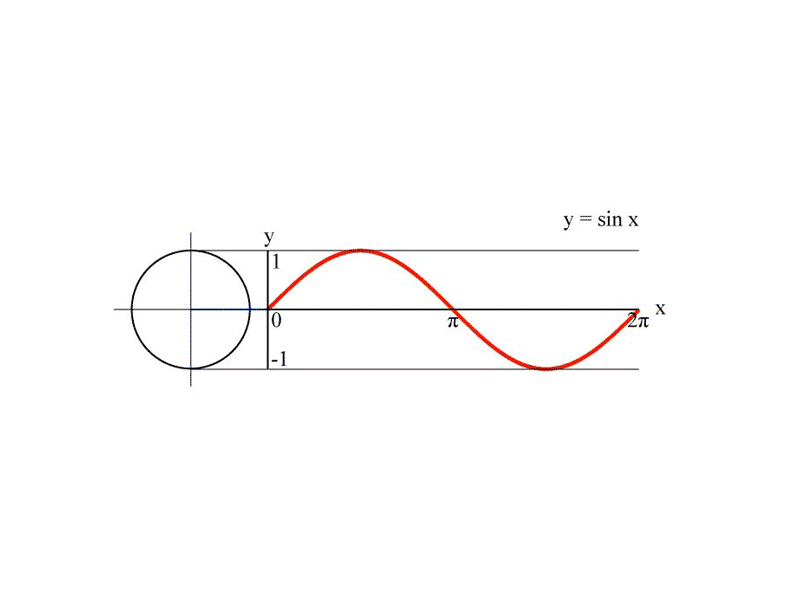
• y ici est la fonction sinus de x, soit \(y=sin(x)\).
  
• x prend comme valeur l’angle d’un cercle en radians.

Le Radian :

Pour commencer, rappelons-nous ce qu’est un radian. Le radian c’est le rapport entre la circonférence et la longueur du rayon. Imaginons un cercle de rayon 1, \(r = 1\). Prenons de sa circonférence un segment d’une longueur égale au rayon du cercle, alors l’angle formé est égal à 1 radian.

Nous savons aussi que la circonférence d’un cercle est égale à son diamètre multiplié par \(\pi\), soit \(\pi \times D\). Donc pour un cercle de rayon 1, appelons-le cercle unité, son diamètre est égal à \(2\times \pi\). Ceci est très bien expliqué par cette animation provenant du site couleur-science.eu.

La formule du signal :

Un signal sinusoïdal est caractérisé par son amplitude maximale et sa fréquence. Il peut s’écrire sous la forme :

\(\large {s(t)=A\,\sin(\omega t+\varphi )}\)

dont :

• \(A\) : amplitude de la grandeur, appelée aussi valeur de crête, dans l’unité de la grandeur mesurée
  
• \(\omega\) : pulsation de la grandeur en rad s⁻¹
  
• \(\omega t + \varphi\) : phase instantanée en rad
  
• \(\varphi\) : phase à l’origine en rad (souvent fixée par l’expérimentateur)

La pulsation, la fréquence et la période sont liées par les relations :

\(\large \omega = 2 \pi f = \frac{2 \pi}{T}\)

4. Explorer la formule

Bon, laissons la notion de phase de côté. Si nous simplifions cette équation, nous obtenons :

\(\large Amplitude * sin(2 * pi * f * t)\)

Expliquons quelque peu cette équation.

L’amplitude :

C’est la distance entre le maximum de l’onde et l’axe y = b (soit l’axe des abscisses si b = 0). Dans notre cas, nous aurons une amplitude de 1.

Le sinus :

Revenons à notre cercle et cette histoire du calcul du sinus d’un angle (exprimé en radian). Prenons par exemple un angle de 90°. Cela équivaut à un angle de \(\frac{\pi}{2}\) rad :

sin(pi / 2)

## [1] 1

Le résultat est égal à 1. Regardez à nouveau la première animation. On peut y apercevoir un triangle rectangle composé d’un côté bleu et un côté orange. Le côté bleu représente l’hypoténuse et l’orange le côté opposé. Le sinus d’un angle dans un triangle rectangle est le rapport entre la longueur du côté opposé à cet angle et la longueur de l’hypoténuse. Lorsque l’angle atteint un angle de 90° ou \(\frac{\pi}{2}\) radian, le rapport entre ce côté et l’hypoténuse vaut 1.

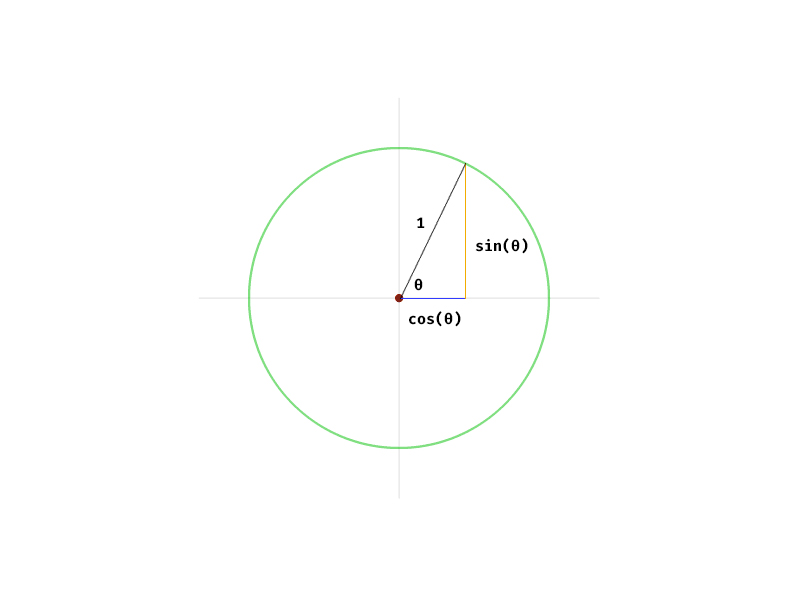
Pour un cercle unité la longueur de l’hypoténuse vaut toujours 1 (son rayon en fait). On peut donc en déduire que le sinus de l’angle équivaut à la longueur du côté opposé :

\(\large sin(\theta)=\frac{opposé}{hypoténuse}=\frac{opposé}{1}\)

Calculons la valeur du sinus pour un angle de 360° :

sin(2 * pi)

## [1] -0.0000000000000002449294

Nous obtenons 0. Même raisonnement.

Ajoutons la fréquence :

Voyons la seconde partie avec \(f\). Il s’agit de la fréquence. La fréquence est le nombre de périodes souhaité ou le nombre de fois ou notre cercle opère une rotation. Ici, l’animation fait 1 tour complet du cercle. Donc la fréquence est de 1.

sin(2 * pi * 1)

## [1] -0.0000000000000002449294

Si nous volons une fréquence de 10 Hz, nous obtenons:

sin(2 * pi * 10)

## [1] -0.000000000000002449294

Le résultat ne change pas. C’est normal puisque après 10 rotations, nous revenons au point de départ où la longueur du côté opposé du triangle retrouve sa valeur initiale.

Passons à t maintenant. t correspond à la valeur de l’angle pour lequel nous voulons calculer le sinus. L’angle est reporté sur l’axe des x représentant la durée de notre onde en seconde. Si en une seconde, notre cercle fait 1 tour, nous aurons une onde de fréquence de 1 Hz, soit pour 1 seconde une valeur comprise entre \(0\) et \(2 \times \pi\). Si notre cercle fait 10 rotations, nous aurons une onde de fréquence de 10 Hz avec une valeur entre \(0\) et \(2 \times \pi \times f\).

Bien, avant d’enregistrer nos valeurs dans un vecteur, revenons à l’échantillonnage. Comme x peut prendre une infinité de valeurs comprises entre \(0\) et \(2 \times \pi \times f\), nous devons échantillonner c’est-à-dire capturer \(x\) valeurs à intervalle défini. Un échantillonnage de 15 Hz correspond à l’enregistrement de 15 valeurs entre \(0\) et \(2\pi f\).

Pour ce faire nous utiliserons la fonction seq() avec l’argument length.out. L’argument length.out découpe l’intervale 0, f en 15 valeurs équidistantes. Commençons par découper notre rotation en 15 valeurs. Pourquoi entre 0 et 1? Et bien parce que nous multiplions chaque valeur par \(2 \times \pi \times f\)

s <- 15
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * 1 * t)

Maintenant que nous avons nos 15 valeurs en radian, affichons le résultat du sinus.

wave %>% str()

##  num [1:15] 0 0.434 0.782 0.975 0.975 ...

Voyons ce que cela donne sur un graphique:

s <- 15
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * 1 * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_segment(aes(x = t, xend = t, y = 0, yend = wave), alpha = .3) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, .5, 1)) +
  scale_x_continuous(breaks = c(0, .5, 1), labels = c("0", "π", "2π")) +
  theme_light()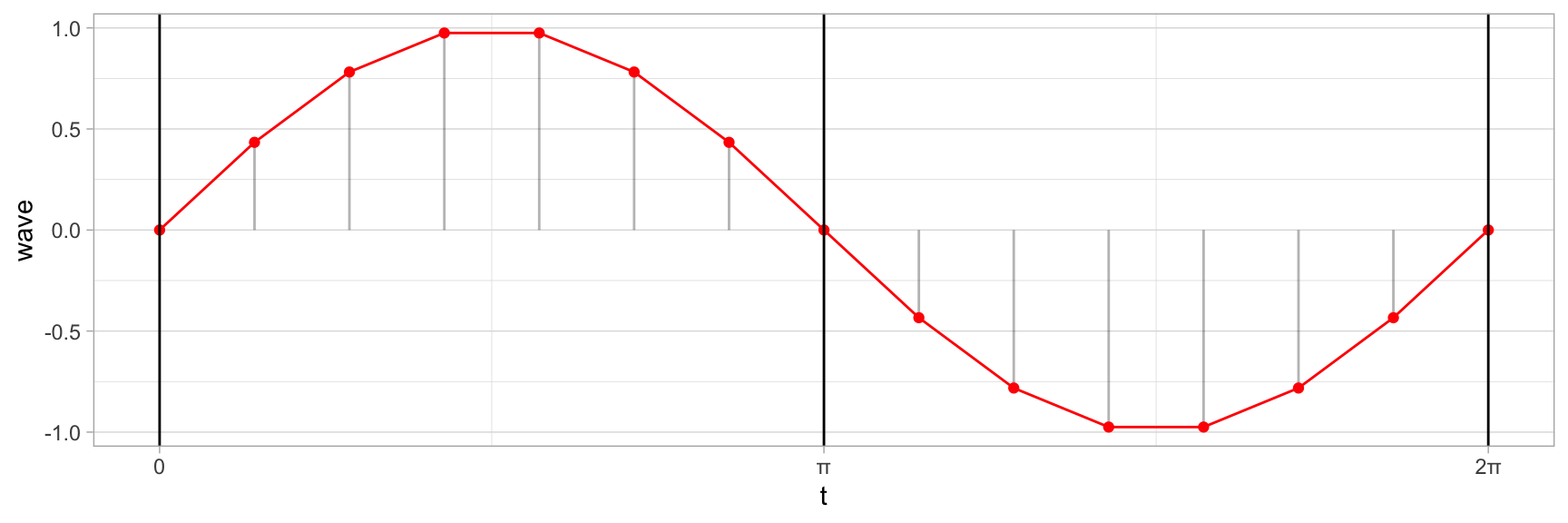

et pour 100 échantillons:

s <- 100
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * 1 * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_segment(aes(x = t, xend = t, y = 0, yend = wave), alpha = .3) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, .5, 1)) +
  scale_x_continuous(breaks = c(0, .5, 1), labels = c("0", "π", "2π")) +
  theme_light()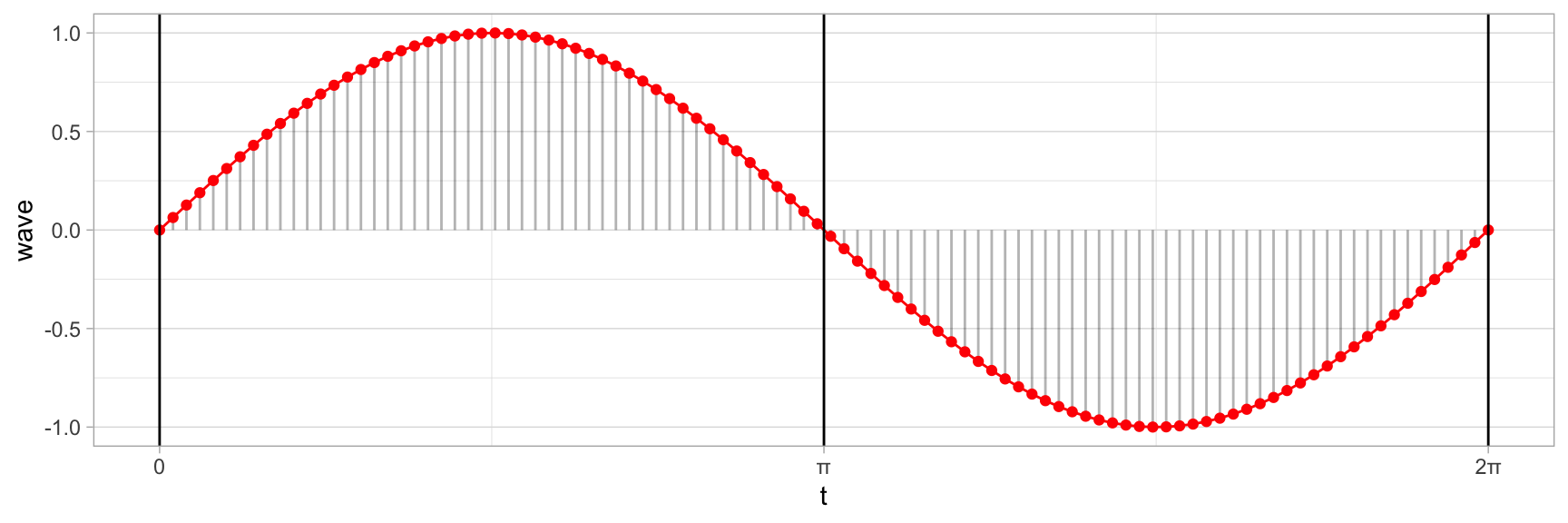

Notre onde est mieux définie. Si nous voulions avoir la qualité CD, il nous faudrait augmenter le nombre d’échantillons à 44,100! Wouah, cela fait 44,100 valeurs pour 1 seconde à une fréquence de 1Hz. On comprend mieux pourquoi un fichier .wav prend de la place. Observez que notre dernière valeur de x est \(2\pi\).

Que faire si nous souhaitons une onde de fréquence de 10Hz? Rappelez-vous de notre formule vue plus haut:

\(Amplitude * sin(2 * pi * f * t)\)

Nous ajoutons une valeur pour la fréquence f et laissons l’amplitude aussi de côté.

f <- 10
s <- 100
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * f * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_segment(aes(x = t, xend = t, y = 0, yend = wave), alpha = .3) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, .5, 1)) +
  scale_x_continuous(breaks = c(0, .5, 1), labels = c("0", "π", "2π")) +
  theme_light()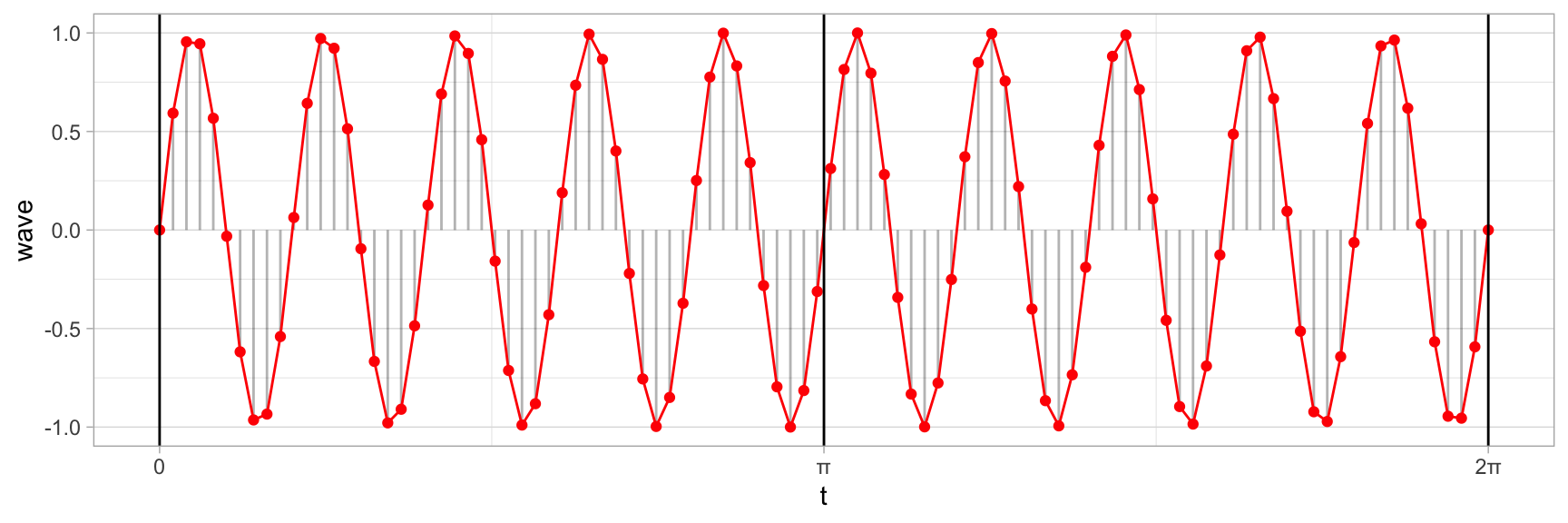

On remarquera que l’échantillonnage se réduit pour chaque période. Il nous faut donc augmenter le nombre d’échantillons pour chaque période. Nous avons 10 périodes, nous pourrions prendre 100 échantillons par période, soit 10 * 100. Pour plus de lisibilité, nous enlevons les segments de notre graphique.

f <- 10
s <- 10 * 100
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * f * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, .5, 1)) +
  scale_x_continuous(breaks = c(0, .5, 1), labels = c("0", "π", "2π")) +
  theme_light()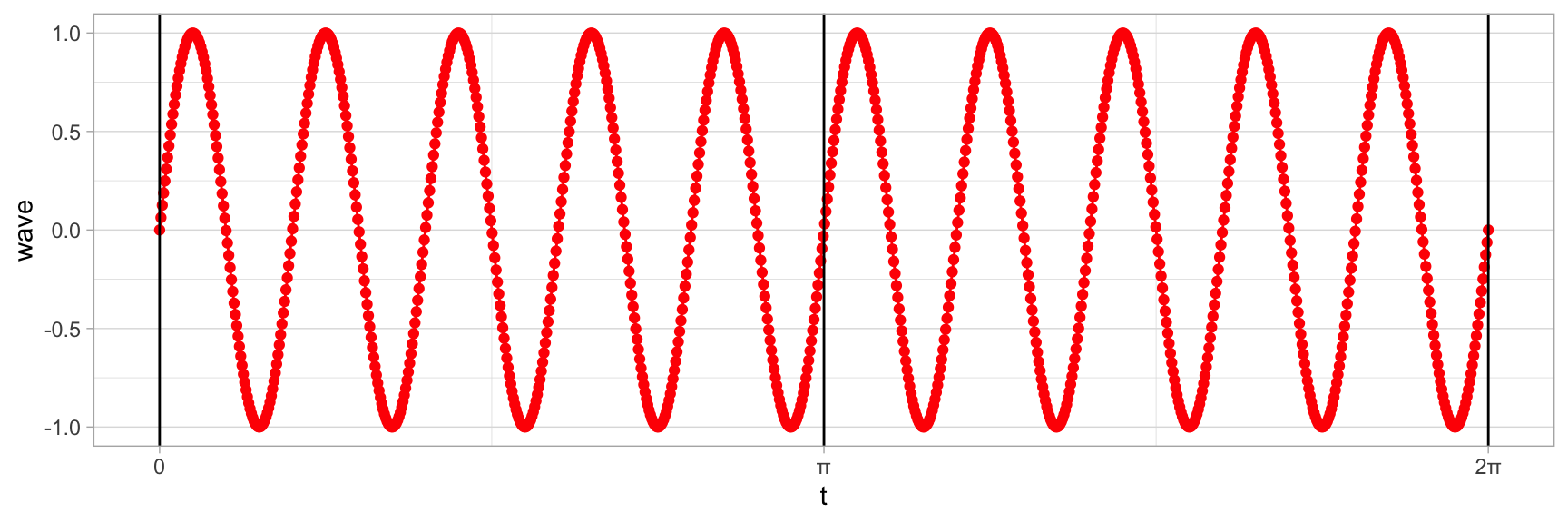

Maintenant nous voulons que l’axe des x soit exprimé en seconde et pas en radians. Nous allons transformer notre table pour en faire une série temporelle. Concrètement nous reportons nos valeurs exprimées en radians sur une échelle de 0 à 1 sec.

f <- 10
s <- 1000
t <- seq(0, 1, length.out = s)

wave <- sin(2 * pi * f * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, 1)) +
  theme_light()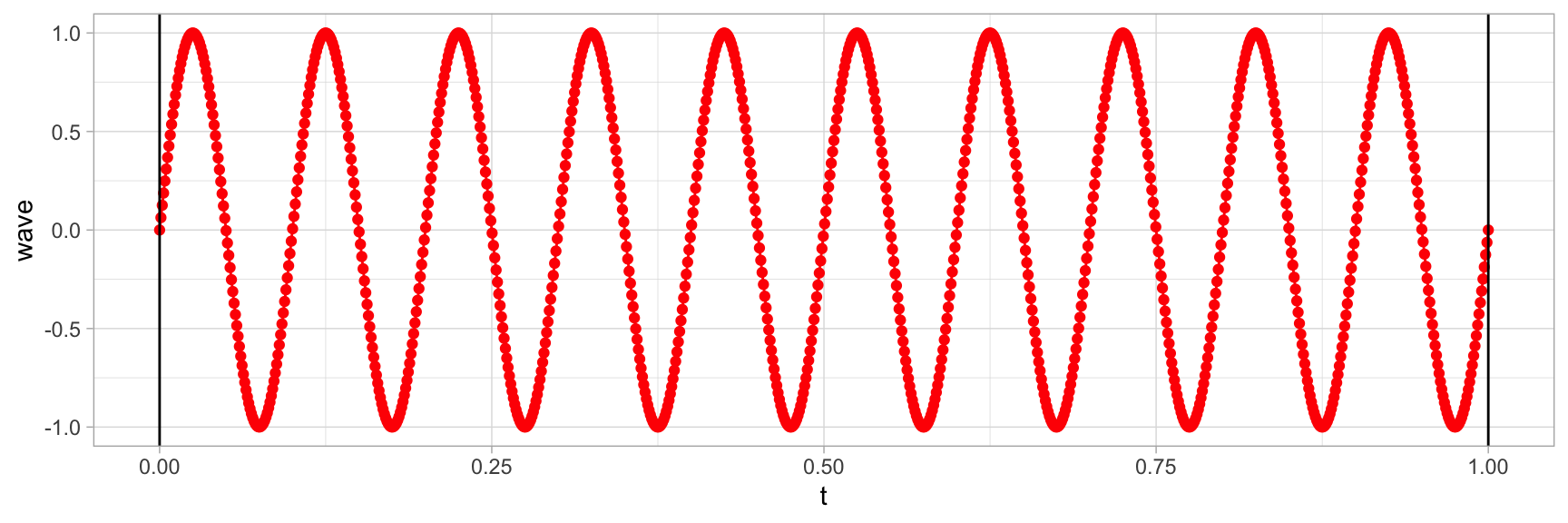

Et si nous voulons une onde de 2 secs? Et bien on ajoute la variable d. Comme nous voulons le nombre d’échantillons pour l’ensemble de la durée, nous remplaçons 1 par d dans la fonction seq() et multiplions s * d pour l’argument. En effet, si nous doublons la durée, nous devons doubler le nombre d’échantillons.

f <- 10
s <- 1000
d <- 2
t <- seq(0, d, length.out = s * d)

wave <- sin(2 * pi * f * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, d)) +
  theme_light()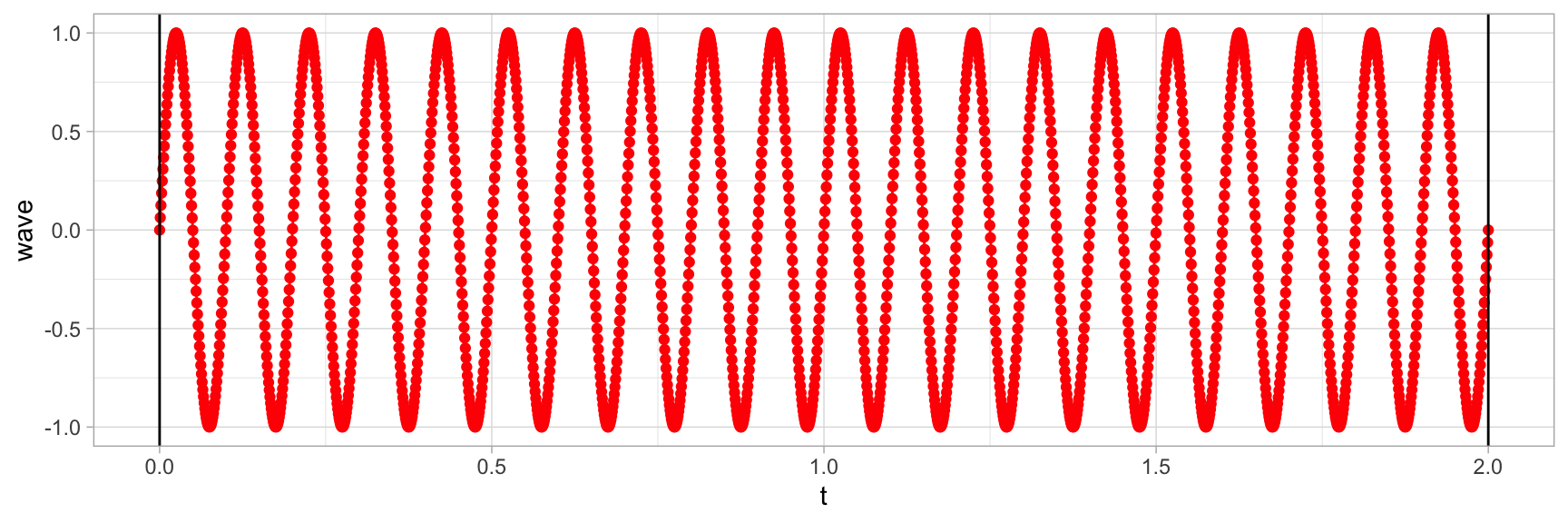

Enfin, pour être complet, ajoutons l’amplitude.

f <- 10
s <- 1000
d <- 2
t <- seq(0, d, length.out = s * d)
a <- 20

wave <- a * sin(2 * pi * f * t)

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, d)) +
  theme_light()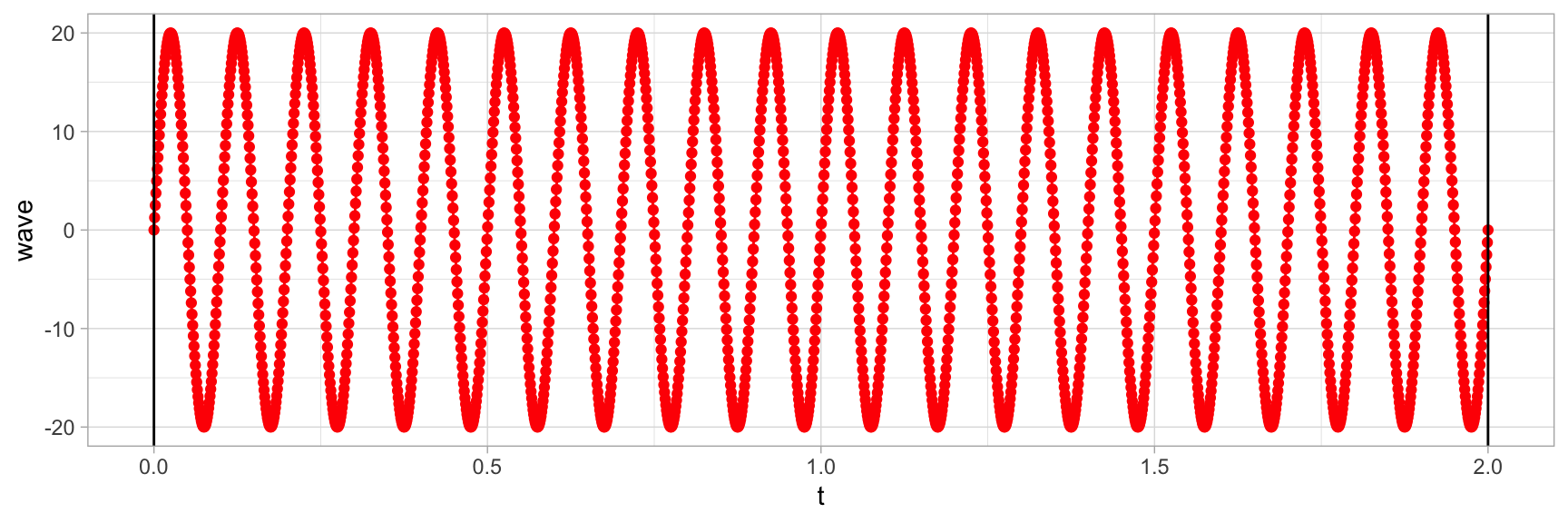

4. Notre fonction

Créons une fonction pour créer notre signal:

my_wave <- function(a, f, d, s, plot = NULL) {
  
t <- seq(0, d, length.out = s * d)

wave <- a * sin(2 * pi * f * t)
  
if(plot) {

tibble(t, wave) %>% 
  ggplot() +
  aes(t, wave) +
  geom_point(colour = "red") +
  geom_line(colour = "red") +
  geom_vline(xintercept = c(0, d)) +
  theme_light()
  
  } else {
    return(wave)
    }

}

Voyons si cela marche:

my_wave(a = 1, f = 10, d = 1, s = 200, plot = TRUE)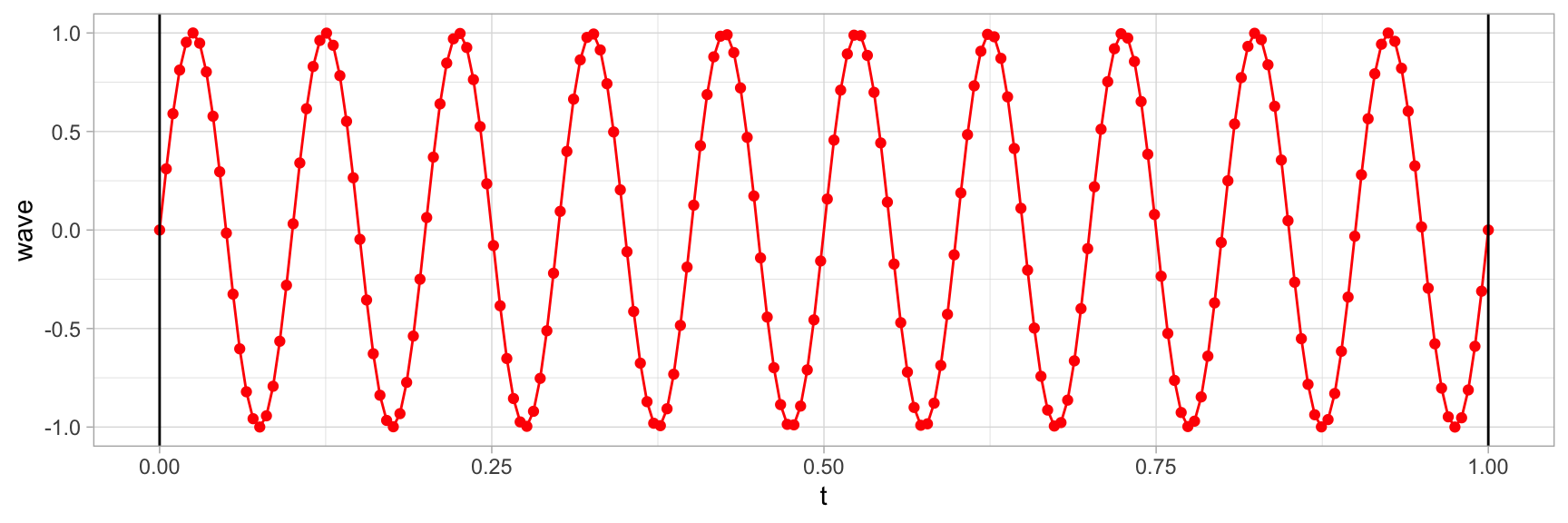

Top! ça marche pas trop mal. Nous pourrions pousser l’exercice un peu plus loin et utiliser la composante geom_function pour ajouter une couche esthétique à ggplot. Pour cela, définissons notre fonction avec as_mapper. La fréquence restera identique. L’échantillonnage sera de 1,000 Hz et définit avec l’argument n = 1000

my_wave2 <- as_mapper(~ sin(2 * pi * 10 * .x))

data.frame(x = c(0, 1)) %>% 
  ggplot() + 
  aes(x) +
  stat_function(fun = my_wave2, geom = "line", n = 1000, colour = "red") +
  geom_vline(xintercept = c(0, 1)) +  
  theme_light()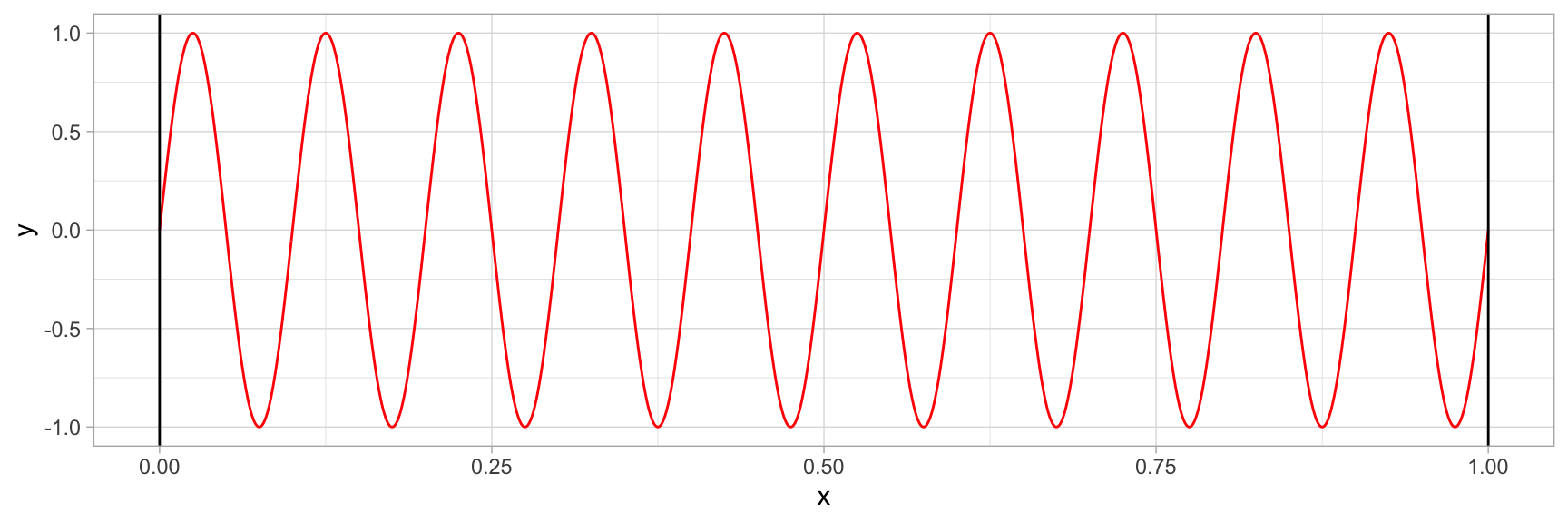

5. Jouer l’onde sonore

Maintenant nous pouvons créer une onde et la faire jouer par R avec la fonction play() du package {tuneR}. Nous choisissons d’abord la fréquence souhaitée pour notre note sonore. Nous partirons sur un la qui a une fréquence de 440 Hz. Spécifions l’échantillonnage de qualité CD soit 44100Hz. Petite subtilité, il faut convertir nos valeurs sur une échelle compatible avec le format .wav avec le fonction normalize(). Nous utiliserons un rescaling 16 bit, c’est à dire un nombre binaire à 16 valeurs soit 2¹⁶. Les valeurs ne seront plus entre [-1,1] mais entre [-32767, 32767]. N’oubliez pas de configurer votre player Wav. Sur Mac, nous utiliserons l’audioplayer cli afplay.

setWavPlayer('/usr/bin/afplay')

note <- my_wave(a = 1, f = 440, d = 1, s = 44100, plot = FALSE)

note_norm <- note %>% Wave(samp.rate = 44100, bit = 16) %>% normalize("16")

note_norm %>% play()

Ceci clôture la première partie de ce post. Vous pouvez écouter le signal enregistré en appuyant sur le bouton play.