MIDI Player avec R | Partie 2

Partie 2. Jouer un fichier MIDI par un instrument et en extraire la mélodie.
L’objectif de cette 2e partie est de créer notre instrument et de jouer une table de fréquence puis de transformer cette table en une mélodie.
Pour les plus paresseux d’entrevous, voici le résultat mais je vous invite à parcourir l’article. C’est un peu long mais je suis sûr que vous découvrirez de nouvelles choses.
1. Le package {seewave}
Pour cette deuxième partie, nous aurons besoin du package {seewave}.
{seewave} offre des fonctions d’analyse, de manipulation, d’affichage,
d’édition et de synthèse des ondes temporelles (en particulier du son).
Pour plus de détails, je vois invite à consulter la documentation sur le site
seewave~. Si vous êtes intéressé par le sujet
sachez qu’un des auteurs, Jérome Sueur à écrit un livre sur le sujet :
Sound Analysis and Synthesis with R.
Ce qui nous intéresse dans le package, c’est la fonction synth().
Cette fonction synthétise un son pur ou harmonique avec une modulation
d’amplitude (am) et/ou une modulation de fréquence (fm).
Nous pourrions nous contenter de notre fonction développée dans la partie 1
mais nous verrons plus loin l’intérêt de la fonction synth().
Elle permet entre autres d’avoir une modulation d’amplitude et de fréquence.
Cela rendra notre instrument plus riche et modulable lorsque nous ferons
notre application Shiny.
library(seewave)2. La fonction synth()
Commençons par afficher l’ensemble des arguments.
synth(f, d, cf, a = 1, signal = "sine", shape = NULL, p = 0,
am = c(0, 0, 0), fm = c(0, 0, 0, 0, 0), harmonics = 1,
plot = FALSE, listen = FALSE, output = "matrix",...)Passons les 4 principaux arguments en revue :
f : la fréquence d’échantillonnage;
d : la durée;
cf : la fréquence;
a : l’amplitude.
Jusqu’ici rien de nouveau… Continuons :
signal : La forme du signal. Par défaut, la forme de l’onde sera sinusoïdale.
Nous avons le choix entre 3 autres fonctions de synthèse : tria, square et saw.
En changeant ces fonctions, nous changeons la nature du son.
shape : Avec cet argument nous sculptons la forme de l’amplitude dans le temps.
Il y a 4 options : incr, decr, sine, tria. C’est en quelque sorte comme si vous
jouiez avec la molette du volume. Vous pouvez augmenter le son, le diminuer,
le moduler.
Laissons am et fm de côté pour l’instant.
À la fin de la partie 1, nous avons synthétisé une onde avec ces paramètres :
a <- 1
cf <- 440
d <- 1
f <- 44100Une onde d’une amplitude : a = 1, d’une fréquence correspondant à la note La :
cf = 440, d’une durée : d = 1 et avec un échantillonnage de qualité CD : f = 44000.
Enregistrons le résultat dans la variable note. Nous précisons aussi le type d’output souhaité : un objet de type “Wave”.
note <- synth(a = a, cf = cf, d = d, f = f, output = "Wave")Le package {seewave} comprend des fonctions de visualisation.
Nous utiliserons 2 fonctions principalement : oscillo() et spectro().
Maintenant que les présentations sont faites, imprimons notre note.
Notre note à une fréquence de 440 Hz. Nous allons donc diviser la durée en 440 pour
ne visualiser qu’une petite partie de l’onde, souvenez-vous, sa période.
Cette période correspond à 1/440 seconde.
note %>% oscillo(f = f, from = 0, to = 1/440) 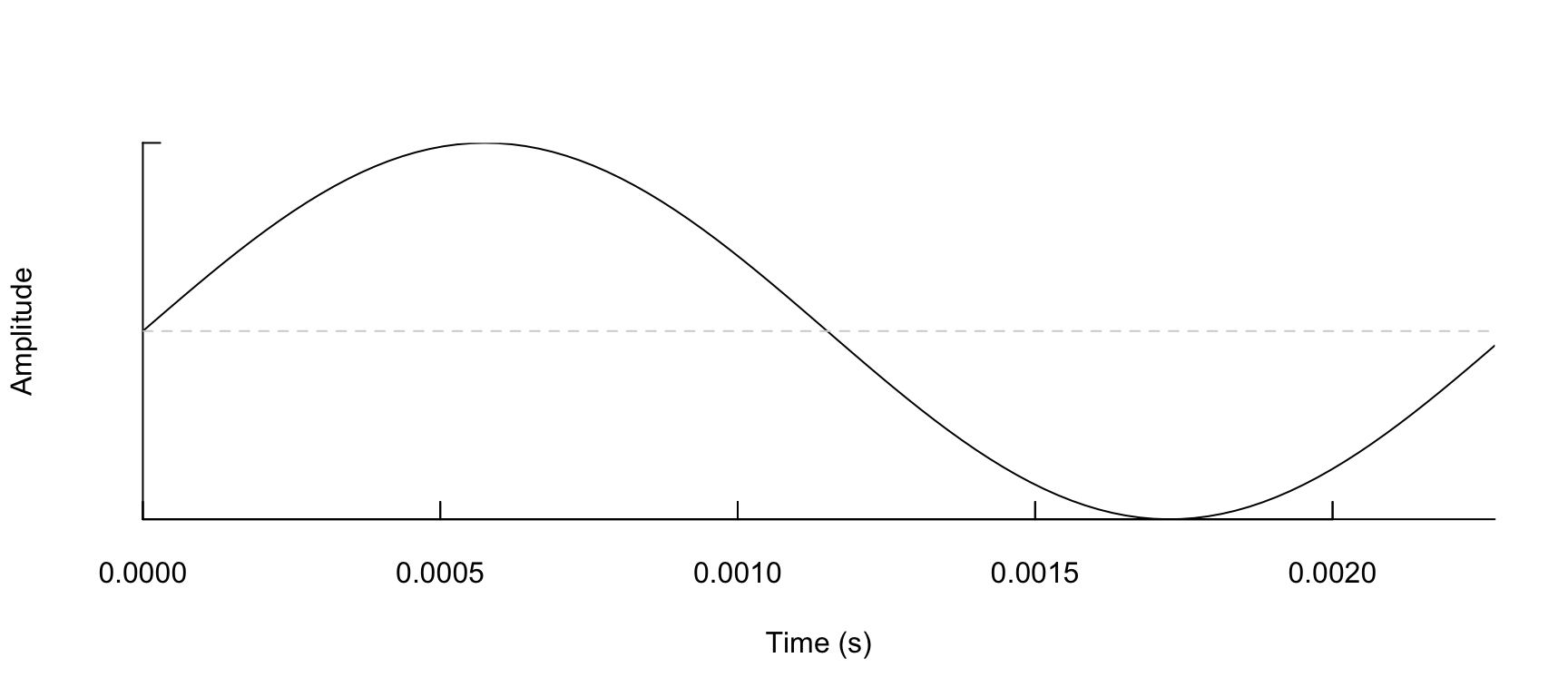
Si nous imprimons la durée complète de l’onde, nous obtenons un graphique difficile à lire.
En effet, nous avons là 440 répétitions d’une période égale à t = 0.0023 secondes.
note %>% oscillo(f = f, from = 0, to = 1) 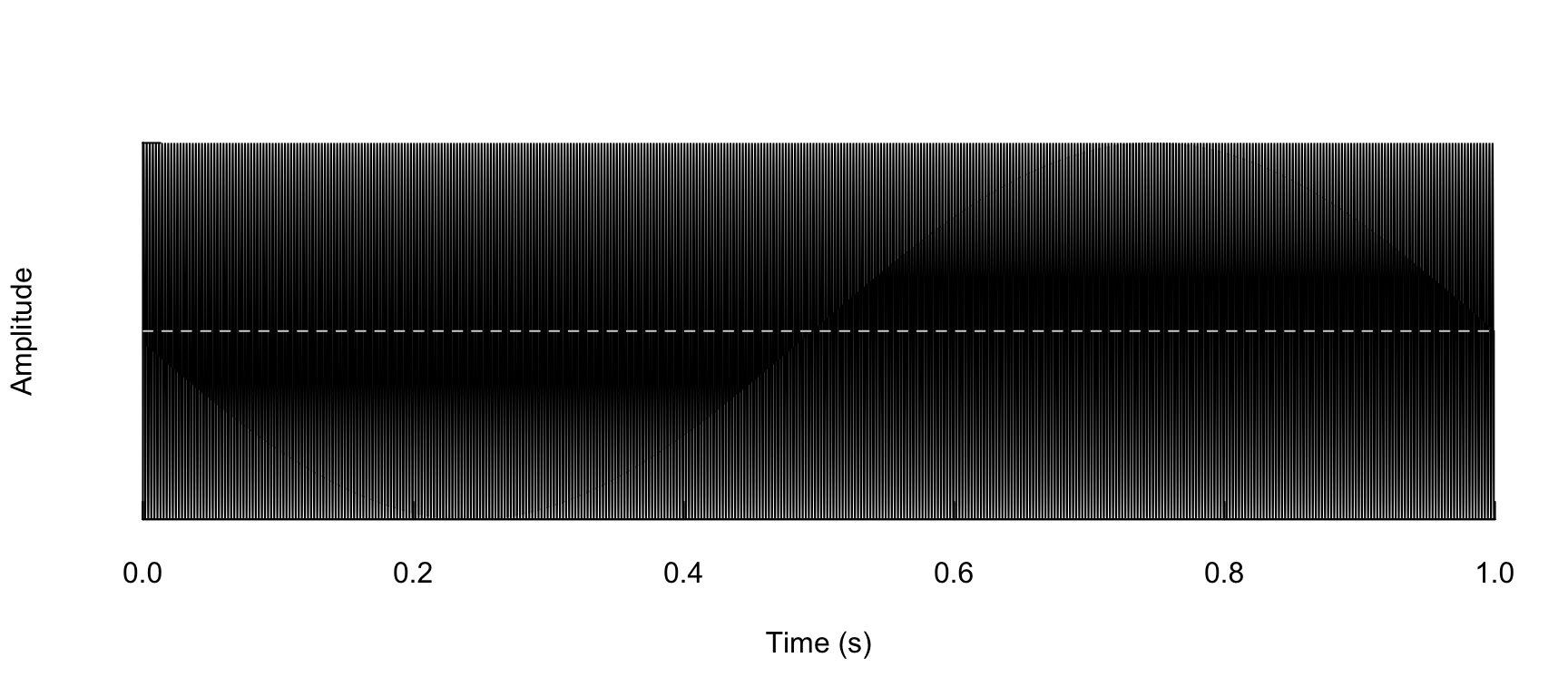
3. Moduler l’amplitude
L’argument shape de la fonction synth() va nous permettre de sculpter l’amplitude et
donner une forme spécifique à l’onde. Voyons les 4 options une à une. Pour bien visualiser
le résultat nous allons réduire la fréquence de l’onde à 50 Hz. Afin d’avoir une onde
audible, nous garderons la fréquence de 440Hz pour l’écoute.
Increasing
note <- synth(a = a, cf = 50, d = d, f = f, shape = "incr", output = "wave")
note %>% oscillo(f = f, from = 0, to = 1) 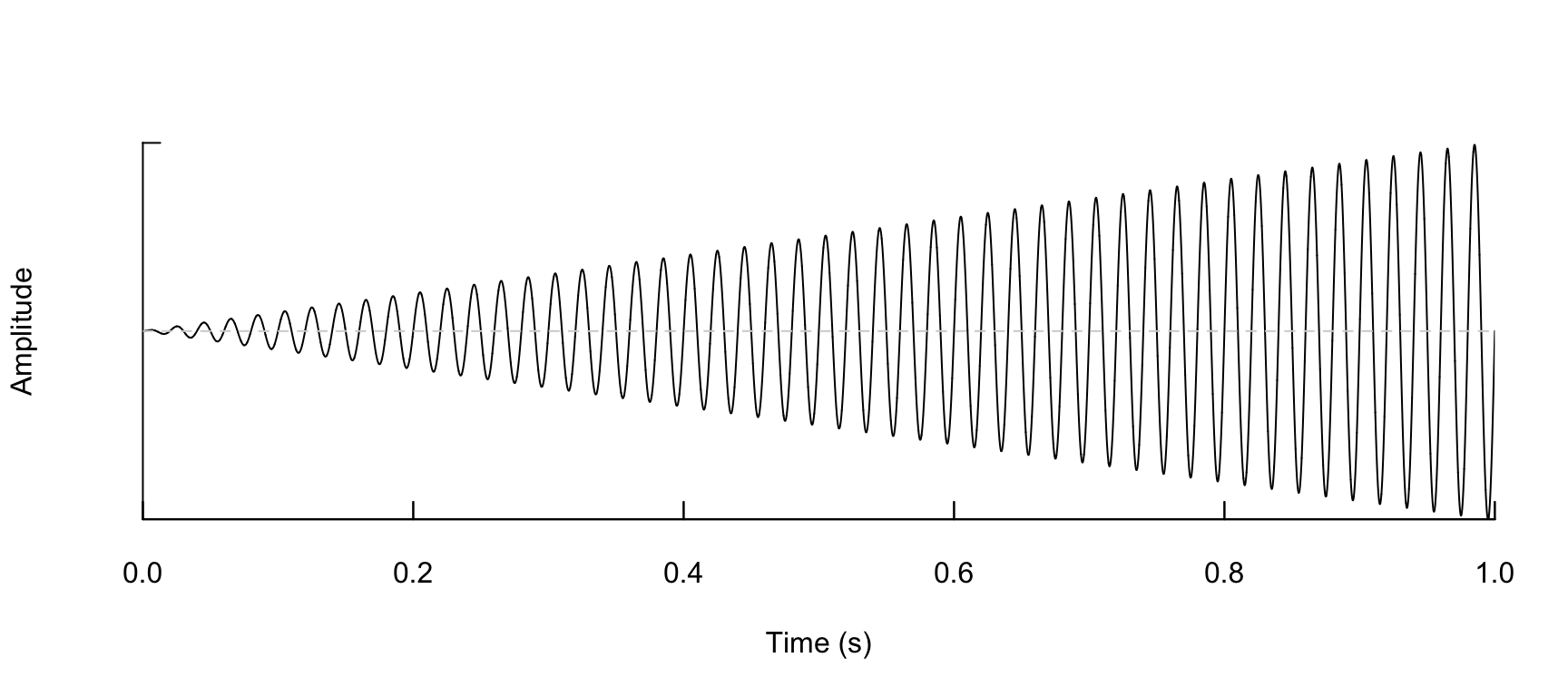
Decreasing
note <- synth(a = a, cf = 50, d = d, f = f, shape = "decr", output = "wave")
note %>% oscillo(f = f, from = 0, to = 1) 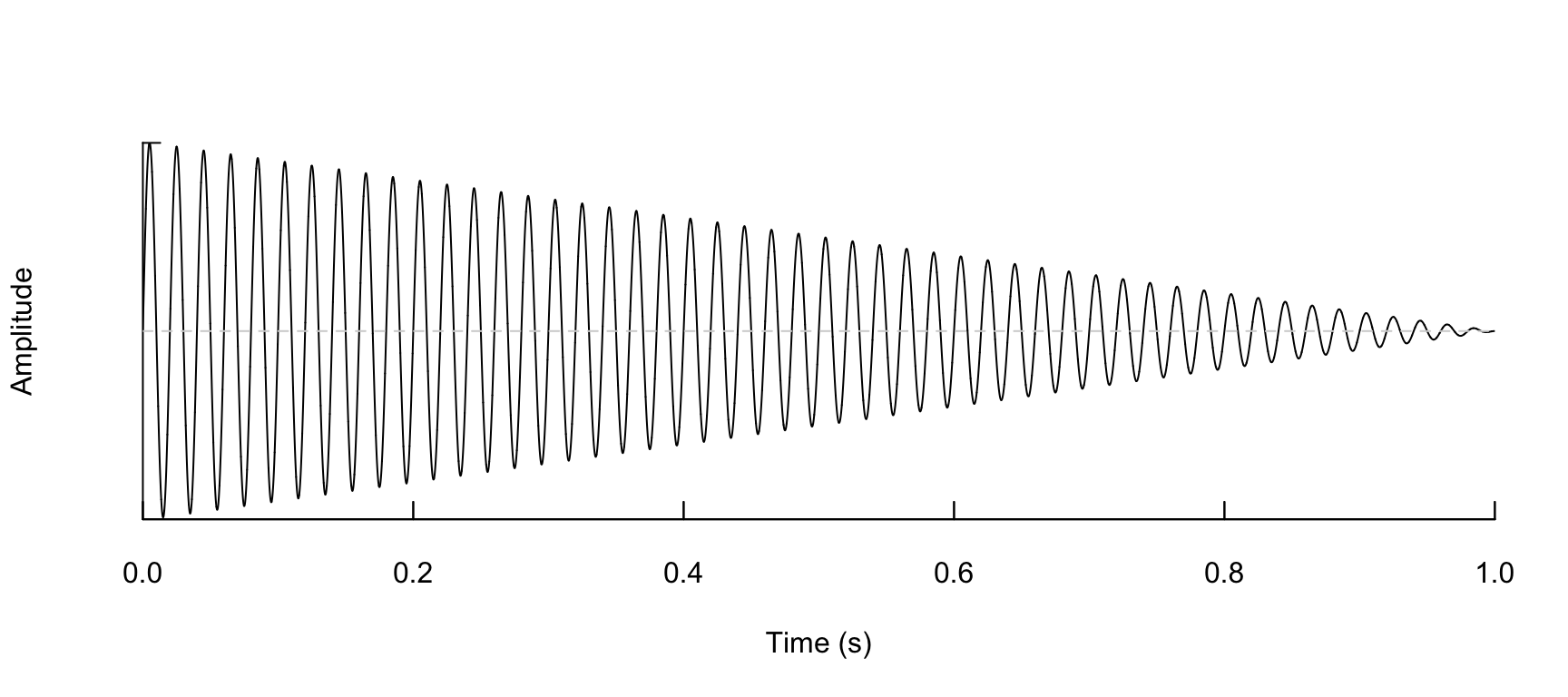
Sine
note <- synth(a = a, cf = 50, d = d, f = f, shape = "sine", output = "wave")
note %>% oscillo(f = f, from = 0, to = 1) 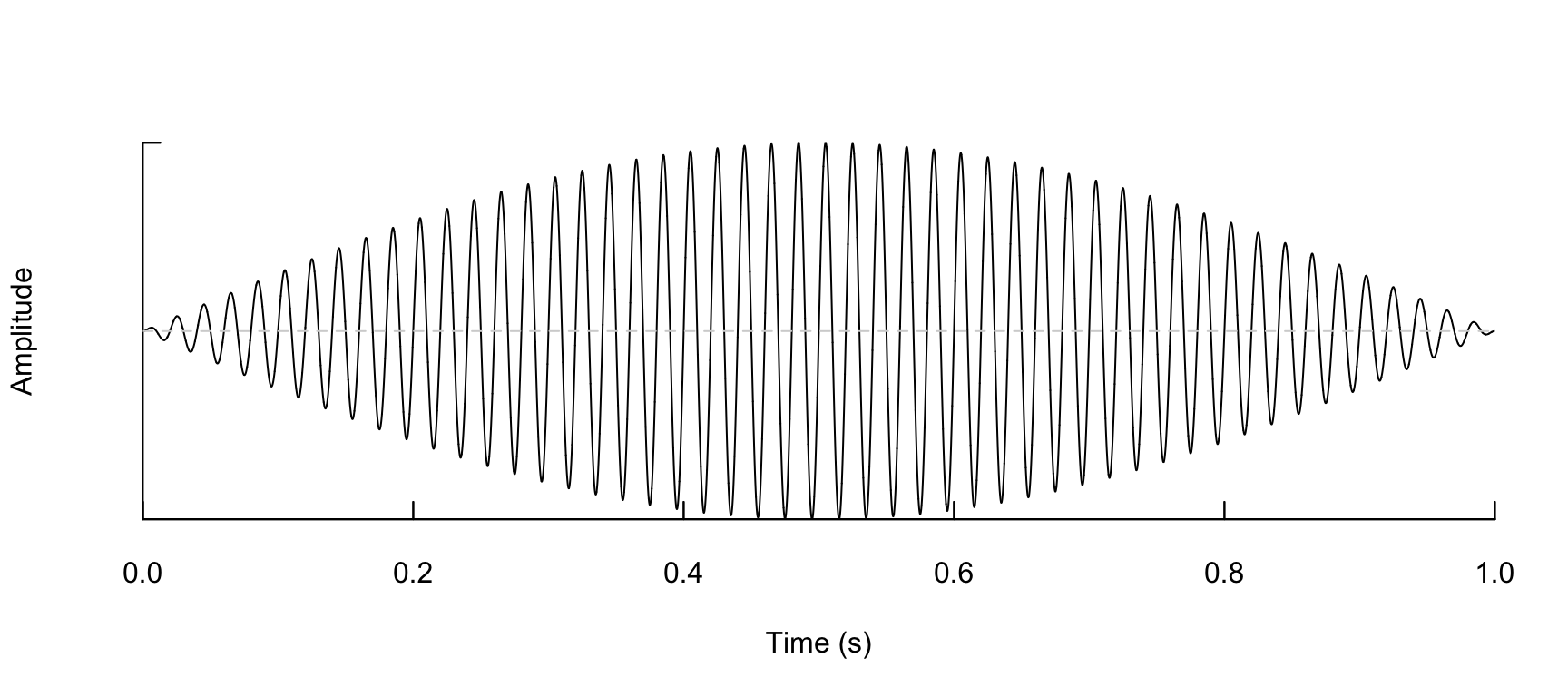
Tria
note <- synth(a = a, cf = 50, d = d, f = f, shape = "tria", output = "wave")
note %>% oscillo(f = f, from = 0, to = 1) 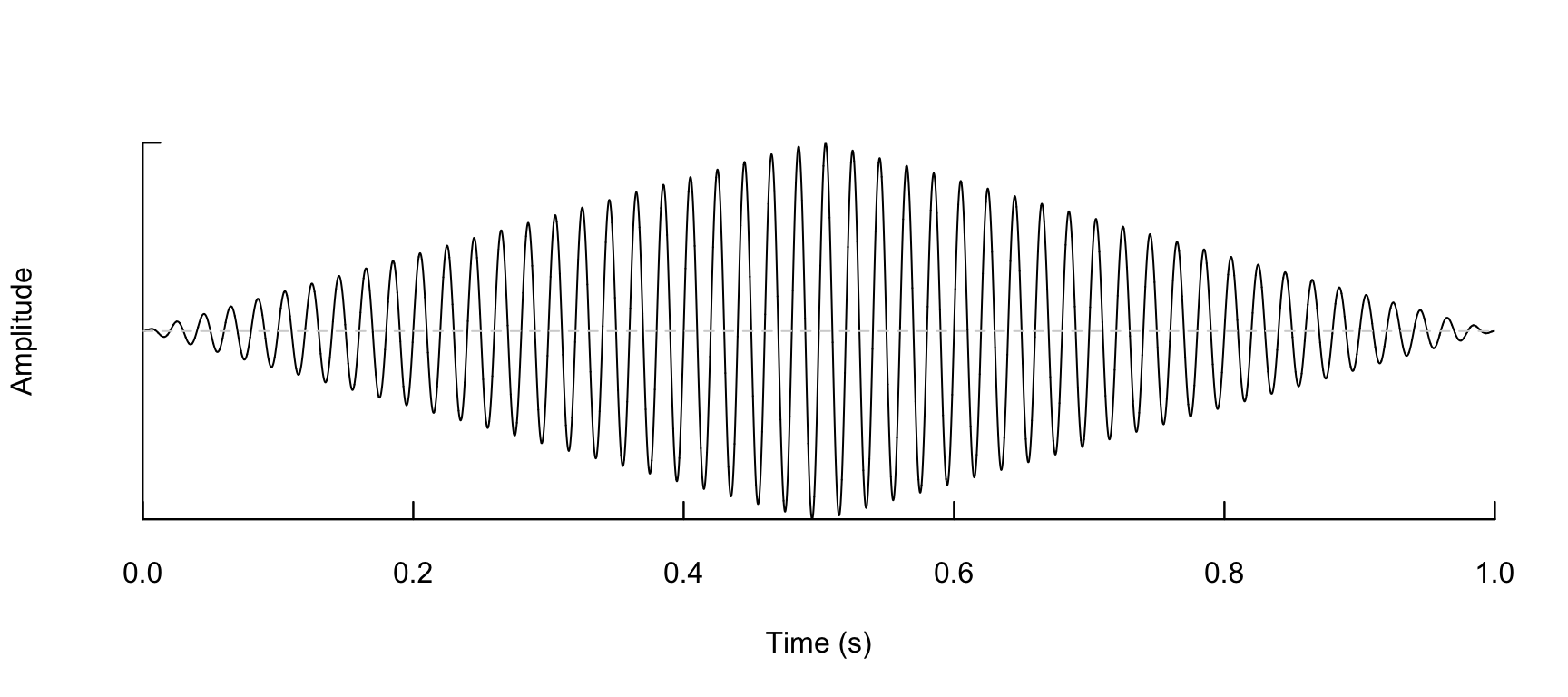
Nous pouvons entendre la différence entre les formes d’ondes.
4. Ajouter des harmoniques
Pour donner plus de profondeur à notre instrument,
nous allons lui ajouter des harmoniques avec l’argument harmonics.
Par défaut, harmonics = 1, ce qui signifie qu’un son pur fait d’une seule harmonique
(fondamentale) sera produit. Pour produire des harmoniques, la longueur du vecteur
doit être supérieure à 1. La longueur déterminera le nombre d’harmoniques,
y compris la première (fondamentale). La valeur de chaque élément du vecteur
précise l’amplitude relative de chaque harmonique.
La première valeur doit être égale à 1.
Nous allons créer un vecteur pour 6 harmoniques avec des valeurs aléatoires sauf pour la première valeur.
harmonics <- c(1, sample(x = seq(0, 1, 0.05), 5, replace = TRUE))
harmonics## [1] 1.00 0.65 0.90 0.30 0.00 0.30Regardons l’onde de plus près. On y voit clairement l’ajout des harmoniques à la note fondamentale.
note <- synth(a = a, cf = 440, d = d, f = f, shape = "sine", output = "Wave", harmonics = harmonics)
note %>% oscillo(f = f, from = 0, to = .01) 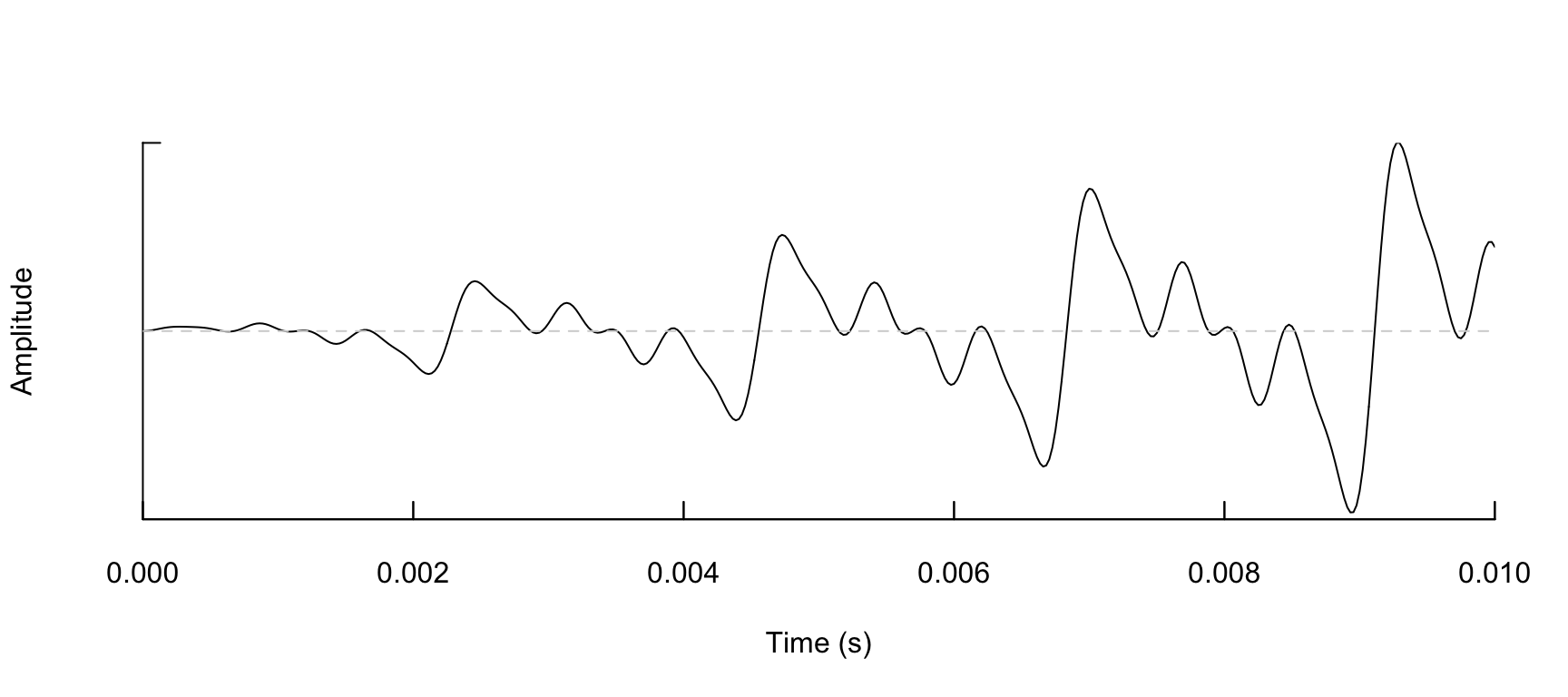
5. La fonction spectro()
Cette fonction renvoie une représentation spectrographique
en deux dimensions d’une onde temporelle. Elle convertit une onde sonore en spectre sonore.
Nous allons utiliser la 2e fonction graphique du package {seewave}.
note %>% spectro(flim = c(0, 3))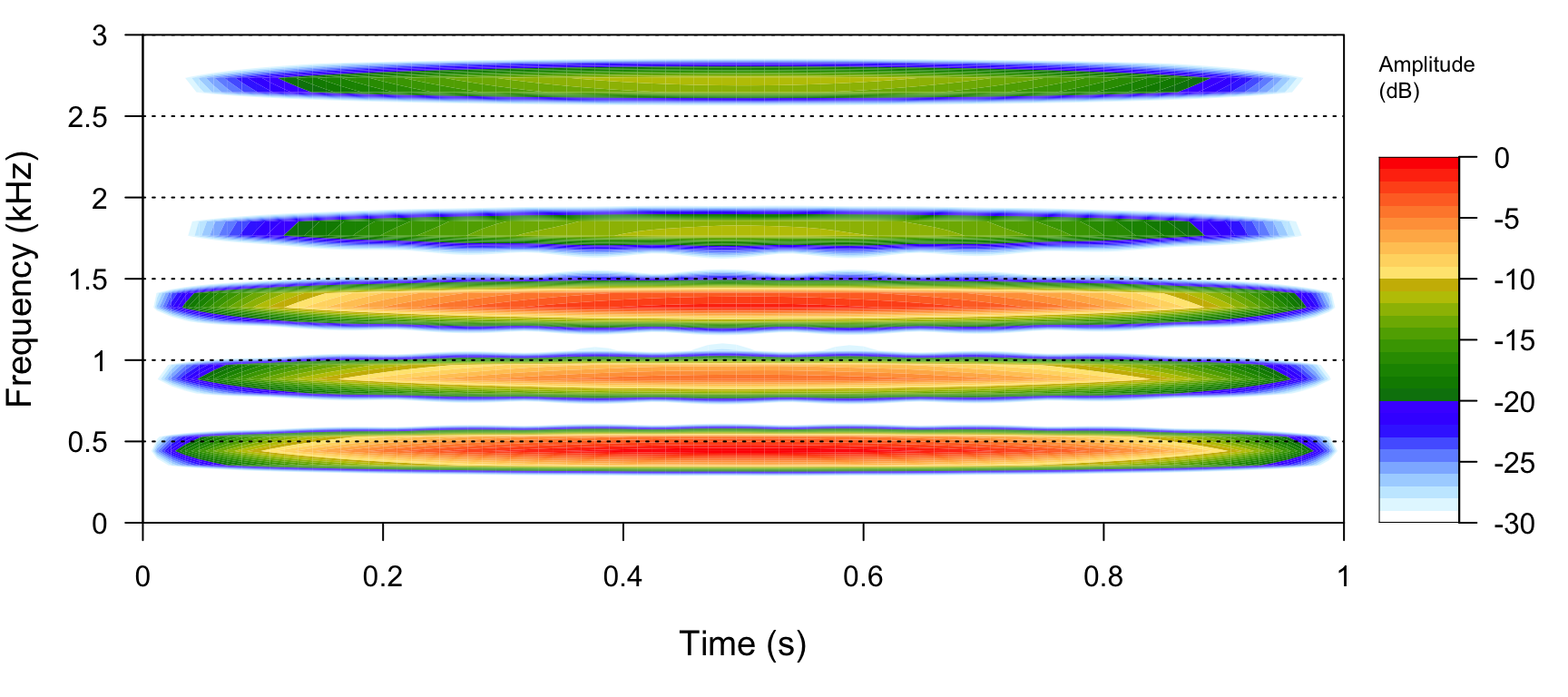 On voit clairement les 5 harmoniques en plus de la fondamentale.
On peut observer aussi la variation de l’amplitude induite par l’argument
On voit clairement les 5 harmoniques en plus de la fondamentale.
On peut observer aussi la variation de l’amplitude induite par l’argument shape.
Affichons à présent la même note, mais sans les harmoniques.
note <- synth(a = a, cf = 440, d = d, f = f, shape = "sine", output = "Wave")
note %>% spectro(flim = c(0, 3))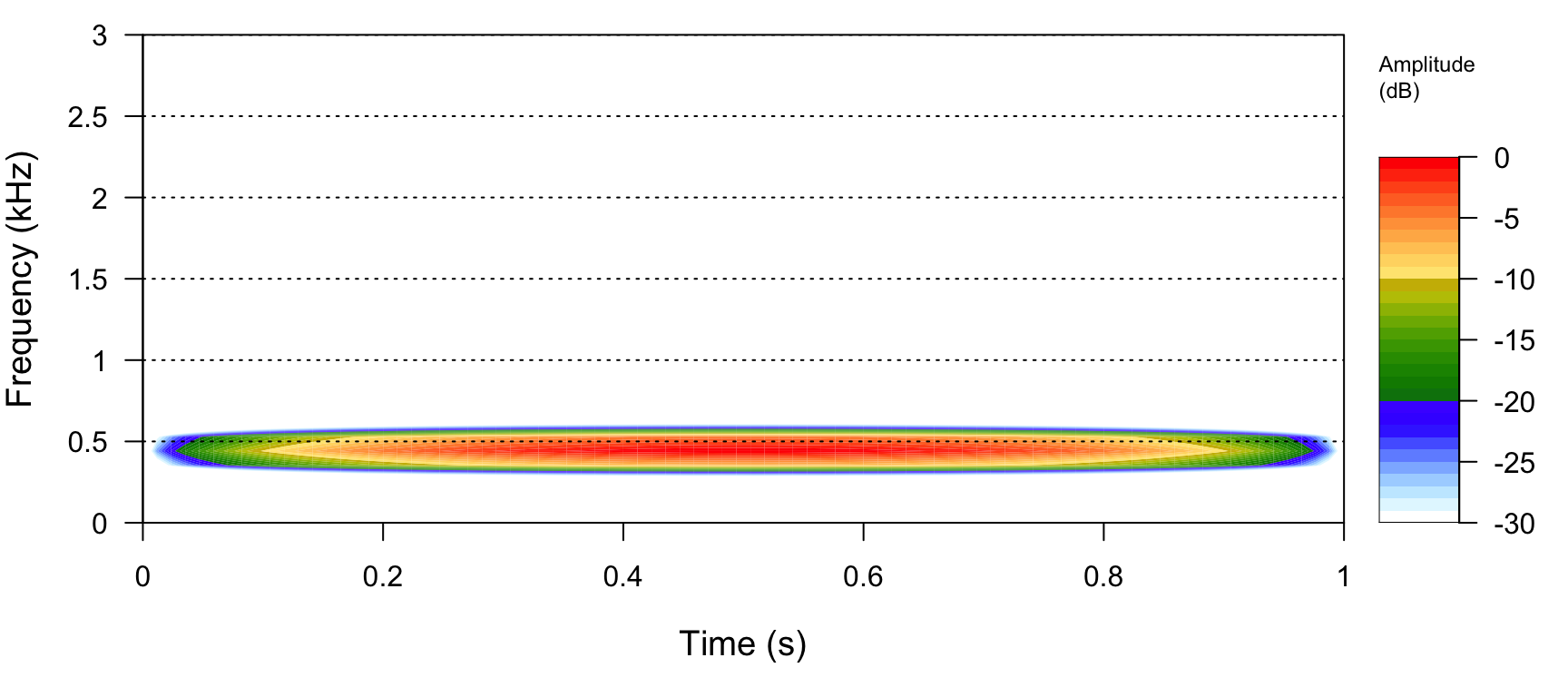 Pas d’harmonique, juste la fondamentale. Maintenant que nous savons comment créer
un instrument, passons à la lecture d’un fichier MIDI.
Pas d’harmonique, juste la fondamentale. Maintenant que nous savons comment créer
un instrument, passons à la lecture d’un fichier MIDI.
6. Lire un fichier MIDI avec {tuneR}
Pour lire un fichier MIDI nous aurons besoin de la fonction readMidi() du package {tuneR}. Une fois le fichier MIDI lu, nous pourrons extraire les notes que nous
transformerons en fréquence. Puis chaque fréquence sera jouée par notre instrument.
Pour ceux qui ne savent pas ce qu’est un fichier MIDI.
Je vous invite à consulter la page wikipedia : MIDI
Les Variations Goldberg
J’aime la musique de Jean-Sébastien Bach. Plus encore Bach joué par Glenn Gould. Glenn Gould à enregistré les Variations Goldberg 2x. En 1955 et en 1980. Deux interprétations différentes que je vous invite à écouter. Certains reconnaitrons d’ailleurs la photo de Gould en cover de cet article. Les variations sont initialement destinées au clavecin à deux claviers, l’usage fréquent de croisements de mains rendant leur interprétation difficile sur un seul clavier. Cela sera donc parfait pour notre Player.
Mutopia Project
Nous téléchargerons les 32 variations sur le site du projet Mutopia.
Aria
Commençons par Aria. Nous utiliserons comme évoqué la fonction readMidi().
midi <- readMidi("data/midifiles/bwv-988-aria.mid")Voyons la structure de notre table.
str(midi)## 'data.frame': 854 obs. of 8 variables:
## $ time : num 0 0 0 0 0 0 0 0 0 0 ...
## $ event : Factor w/ 27 levels "Note Off","Note On",..: 13 11 11 25 23 22 13 5 5 14 ...
## $ type : chr "03" "01" "01" "58" ...
## $ channel : num NA NA NA NA NA NA NA 0 0 NA ...
## $ parameter1 : int NA NA NA NA NA NA NA 6 6 NA ...
## $ parameter2 : int NA NA NA NA NA NA NA NA NA NA ...
## $ parameterMetaSystem: chr "control track" "creator: " "GNU LilyPond 2.16.1 " "3/4, 18 clocks/tick, 8 1/32 notes / 24 clocks" ...
## $ track : int 1 1 1 1 1 1 2 2 2 2 ...Difficile de faire quelque chose avec cela. Pour faciliter les choses,
nous utiliserons la fonction getMidNotes() qui nous permettra d’extraire les notes
de notre table d’événements MIDI.
midinotes <- getMidiNotes(midi)
str(midinotes)## 'data.frame': 418 obs. of 7 variables:
## $ time : num 0 384 768 1056 1152 ...
## $ length : num 384 384 288 96 170 21 170 21 768 384 ...
## $ track : int 2 2 2 2 2 2 2 2 2 2 ...
## $ channel : num 0 0 0 0 0 0 0 0 0 0 ...
## $ note : int 79 79 81 83 81 79 78 76 74 67 ...
## $ notename: Factor w/ 132 levels "C,,,","C#,,,",..: 80 80 82 84 82 80 79 77 75 68 ...
## $ velocity: int 90 90 90 90 90 90 90 90 90 90 ...Nous voyons que la table comprend plusieurs variables :
time : Le moment ou la note est enclenchée;
length : La durée de la note en question;
track : La piste ou se trouve la note;
channel : Le canal MIDI;
note : la note qui doit être jouée par l’instrument;
notename : Le nom de la note;
velocity : La force de frappe.
Seulement comment transformer la valeur de la variable note en fréquence ?
Table de fréquence
En cherchant un peu, j’ai trouvé sur le web une page qui reprend la fréquence pour
chaque valeur de note MIDI sous forme de table.
Nous allons scrapper la table présente sur la page avec la fonction read_html() du package {rvest}.
Si vous souhaitez en savoir plus sur le scrapping, je vous invite à lire mon post sur le scrapping de données :
Scraping de données avec Purrr.
La fonction clean_names() du package {janitor} est aussi utilisée. Elle permet de nettoyer
les noms des variables de la table.
note_table <- read_html("http://www.tonalsoft.com/pub/news/pitch-bend.aspx")
note_table_cleaned <- note_table %>%
html_table(header = TRUE) %>%
map_dfr(., ~ mutate_if(., is.numeric, as.character)) %>%
clean_names() %>%
select(midi_note_number, frequency_hz) %>%
transmute(note = midi_note_number, freq = parse_number(frequency_hz)) %>%
mutate(note = as.numeric(note))
saveRDS(note_table_cleaned, "note_table_cleaned.Rds")Affichons le résultat :
head(note_table_cleaned)## note freq
## 1 127 12543.854
## 2 126 11839.822
## 3 125 11175.303
## 4 124 10548.082
## 5 123 9956.063
## 6 122 9397.273Nous avons obtenu pour chaque valeur MIDI la fréquence correspondante.
7. Monophonique ou polyphonique
Bien, passons à la partie compliquée. Oui, jusqu’ici c’était assez simple. Essayons d’abord avant de passer au script, de bien comprendre ce que nous devons faire. Si nous visualisons notre fichier MIDI sous forme d’un pianoroll, nous comprendrons exactement ou se trouve la difficulté d’interpréter la table.
midinotes %>%
# filter(channel == 0) %>%
filter(time < (384 * 15)) %>%
mutate(end = time + length) %>%
ggplot() +
aes(time, notename, col = as.factor(notename), group = time) +
geom_segment(aes(x = time, xend = end, y = notename, yend = notename), size = 8) +
geom_segment(aes(x = time, xend = (time + 20), y = notename, yend = notename), size = 8, col = "black") +
# scale_x_continuous(breaks = seq(0, (384 * 40), 384), guide = guide_axis(n.dodge = 2)) +
geom_segment(aes(x = time, xend = end, y = notename, yend = notename), size = 1, col = "black", linejoin = "mitre") +
# geom_vline(aes(xintercept = time)) +
theme_minimal() +
theme(legend.position = "NONE") +
facet_grid(channel ~ ., scales = "free")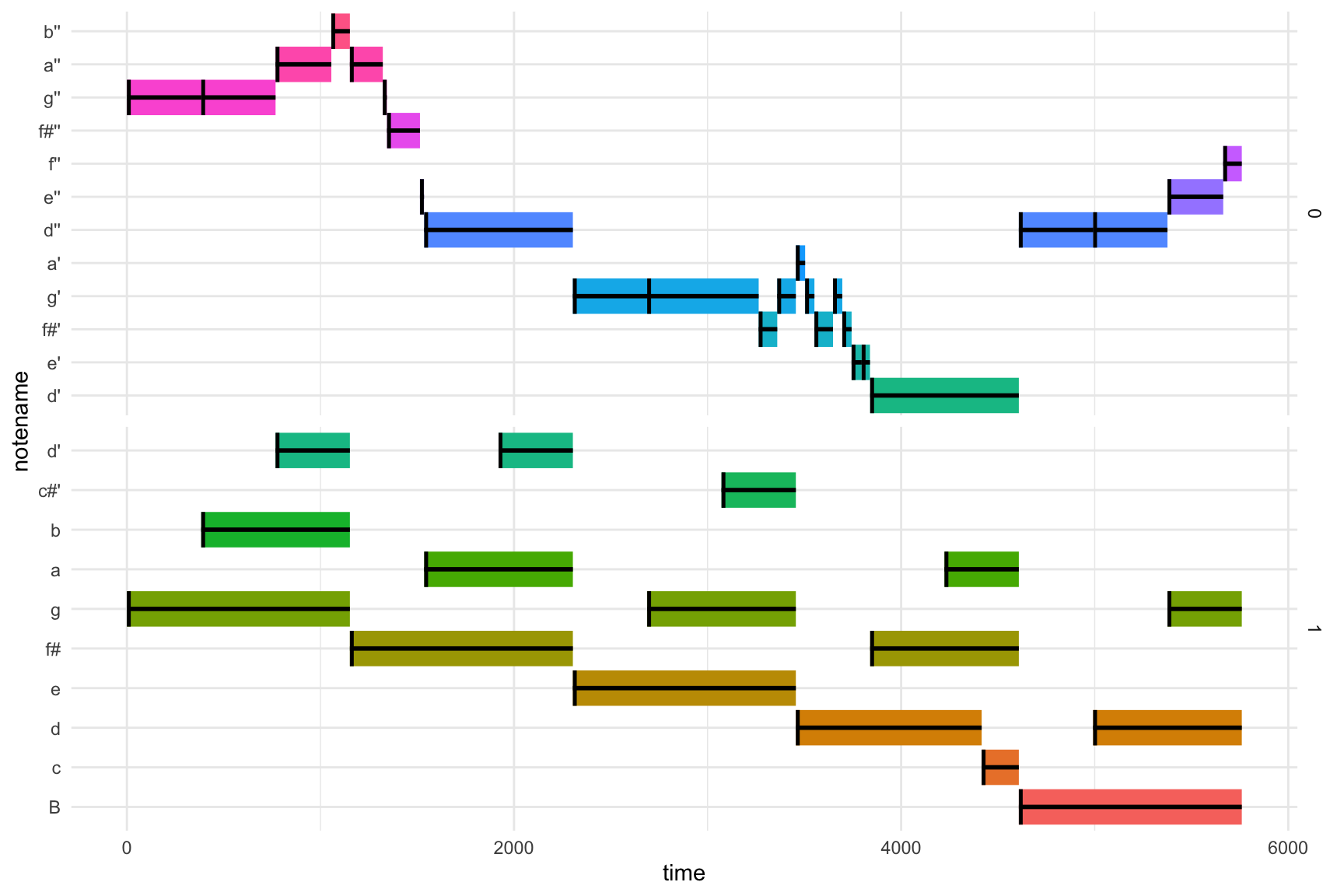 Première chose, nous avons pour chaque note des moments où la note est jouée puis des moments
où la note n’est pas jouée et donc silencieuse.
Première chose, nous avons pour chaque note des moments où la note est jouée puis des moments
où la note n’est pas jouée et donc silencieuse.
Puis, plusieurs note peuvent être jouées en même temps. Ce qui demande donc à l’instrument d’être capable de jouer ces notes une sur l’autre. Ce qui permet de jouer la main gauche et la main droite en même temps. D’où la notion d’instrument polyphonique, comme le piano, versus un instrument monophonique comme la flûte où une seule note est jouée à la fois.
8. L’approche
L’approche consiste donc à :
- Synthétiser une onde pour une note selon sa durée et sa fréquence (par ex. la note
79);
- Synthétiser les silences pour la note en question;
- Raccorder les ondes et les silences pour avoir une onde complète pour la note de la durée du morceau;
- Recommencer le principe pour chaque note qui compose notre partition.
Pour bien comprendre, imaginez que le morceau est composé d’une seule note jouée plusieurs fois de façon successive pendant une période donnée. Chaque fois que la note est frappée, nous synthétisons une onde d’une durée équivalente à la durée ou la note est maintenue sur le clavier. Puis lorsque celle-ci est relâchée, nous synthétisons un silence. Enfin nous attachons ensemble, comme des wagons d’un train, chaque note et silence pour obtenir une onde de longueur équivalente à notre morceau.
Vous l’avez compris, nous ferons une boucle sur chaque note avec la fonction map() du package {purrr}.
Mais avant d’itérer la fonction de synthèse d’onde et de silence sur chaque note, il faut la composer.
Allons-y!
9. Les notes
Etape 1
Travaillons d’abord sur une note en particulier. Par ex. la note 79 de la piste 2.
- Nous transformons la table en tibble avec
as_tibble().
- Nous gardons que les colonnes qui nous intéressent avec
select(-channel, -notename, -velocity).
- Nous filtrons la piste et la note avec
filter(track == 2, note == 79).
note_1 <- midinotes %>%
as_tibble() %>%
select(-channel, -notename, -velocity) %>%
filter(track == 2, note == 79)
head(note_1)## # A tibble: 6 x 4
## time length track note
## <dbl> <dbl> <int> <int>
## 1 0 384 2 79
## 2 384 384 2 79
## 3 1322 21 2 79
## 4 6912 48 2 79
## 5 7152 144 2 79
## 6 11520 384 2 79Etape 2
Avec la fonction transmute() nous calculons une nouvelle variable et renommons d’autres :
noterestenotemais mis en 1e position.
trackrestetrackmis en 2e position.
note_onindiquera quand la note est frappée dans le temps en millisecondenote_on = time.
note_offindiquera quand la note est lâchée dans le temps en millisecondenote_off = time + length.
note_lengthla durée du maintient de la notenote_length = length.
note_2 <- note_1 %>%
transmute(note, track, note_on = time, note_off = time + length, note_length = length)
head(note_2) ## # A tibble: 6 x 5
## note track note_on note_off note_length
## <int> <int> <dbl> <dbl> <dbl>
## 1 79 2 0 384 384
## 2 79 2 384 768 384
## 3 79 2 1322 1343 21
## 4 79 2 6912 6960 48
## 5 79 2 7152 7296 144
## 6 79 2 11520 11904 384Etape 3
Nous ajoutons une colonne avec la fréquence correspondant à la note en question
avec la fonction left_join(note_table_cleaned, by = "note").
Concrètement nous joignons cette table avec la table note_table_cleaned enregistrée plus haut.
note_3 <- note_2 %>% left_join(note_table_cleaned, by = "note") %>%
select(note, note_on, note_length, freq)
head(note_3)## # A tibble: 6 x 4
## note note_on note_length freq
## <dbl> <dbl> <dbl> <dbl>
## 1 79 0 384 784.
## 2 79 384 384 784.
## 3 79 1322 21 784.
## 4 79 6912 48 784.
## 5 79 7152 144 784.
## 6 79 11520 384 784.Etape 4
Pour chaque observation de notre table, nous mappons la fonction synth() avec
la fonction map2(). map2() nous permet d’utiliser 2 valeurs de la table pour la fonction.
Les 2 valeurs utiles sont freq et note_length. Pour synthétiser notre onde,
nous utilisons les valeurs suivantes :
- Un échantillonnage de 8,000 Hz
f <- 8000.
- La fréquence égale à
cf <- .x.
- La durée égale à
d <- .y/384ce qui nous donnera une onde de 1sec pour les notes dont la valeur égale 384.
- Une forme sinus pour l’amplitude
shape <- "sine".
- L’ajout d’un harmonique
harmonics <- c(1, 0.5).
- Un objet de classe
Wave.
Pour faciliter la lecture, nous créons une fonction synth_note() avec des valeurs
sur-mesure pour nos arguments. N’oublions pas d’indiquer avec .x et .y quelles
variables de notre table utiliser pour la fonction. Ici logiquement la fréquence et la durée.
harmonics <- c(1, sample(x = seq(0, 1, 0.05), 5, replace = TRUE))
synth_note <- as_mapper(~ synth(f = 8000,
cf = .x,
d = .y/384,
shape = "sine",
harmonics = harmonics,
output = "Wave"
)
)
note_4 <- note_3 %>% mutate(synth = map2(freq, note_length, ~synth_note(.x, .y)))
head(note_4)## # A tibble: 6 x 5
## note note_on note_length freq synth
## <dbl> <dbl> <dbl> <dbl> <list>
## 1 79 0 384 784. <Wave>
## 2 79 384 384 784. <Wave>
## 3 79 1322 21 784. <Wave>
## 4 79 6912 48 784. <Wave>
## 5 79 7152 144 784. <Wave>
## 6 79 11520 384 784. <Wave>Etape 5
Pour vérifier que la procédure fonctionne, nous additionnons chaque onde
en mappant la fonction bind() avec reduce(). Cela consiste à combiner
chaque onde une dernière l’autre. Pour reprendre la métaphore du train,
c’est constituer notre suite de wagons.
Pour bien comprendre la fonction reduce() qui enveloppe la fonction bind(),
voici un petit exemple. Comme nous ne pouvons pas utiliser la fonction bind()
sur un vecteur nous utiliserons sum() mais le principe reste le même :
c(1, 2, 3) %>% reduce(sum)## [1] 6Rappelez-vous seulement que nous n’avons pas encore de wagon silence.
Donc chaque note sera jouée une derrière l’autre.
note_5 <- note_4 %>%
select(synth) %>%
unlist() %>%
reduce(bind) Voyons ce que cela donne sur le spectrogramme.
note_5 %>% spectro()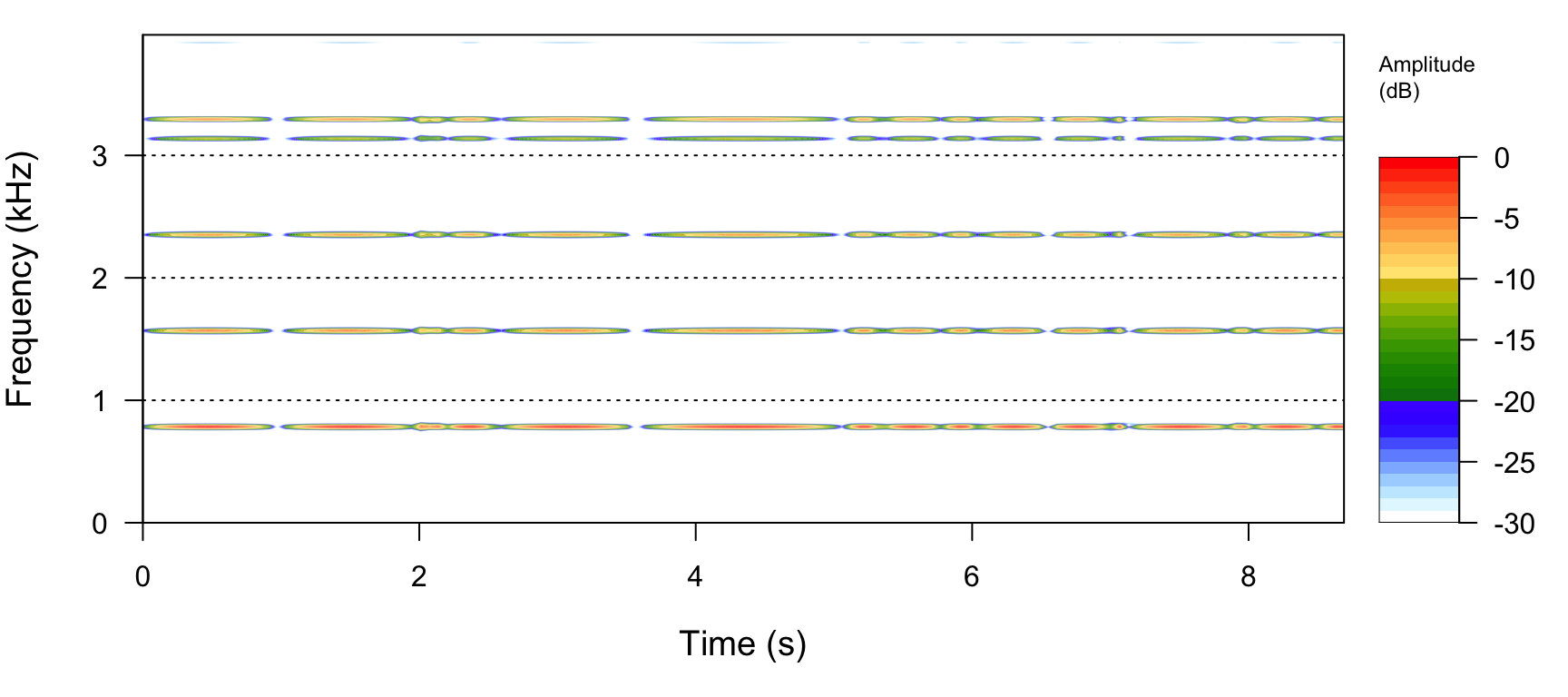
10. Les silences
Passons aux silences. Une mélodie est constituée de notes mais aussi de silences. Nous procédons à la même approche que pour les notes avec deux différences :
- la fonction
synth()sera remplacée par la fonctionaddsilw().
- le durée des silences doit être calculée au préalable.
Etape 1
Pas de changement pour l’étape 1
silence_1 <- midinotes %>%
as_tibble() %>%
select(-channel, -notename, -velocity) %>%
filter(track == 2, note == 79)
head(silence_1)## # A tibble: 6 x 4
## time length track note
## <dbl> <dbl> <int> <int>
## 1 0 384 2 79
## 2 384 384 2 79
## 3 1322 21 2 79
## 4 6912 48 2 79
## 5 7152 144 2 79
## 6 11520 384 2 79Etape 2
Pas de changement pour cette étape.
silence_2 <- silence_1 %>%
transmute(note, track, note_on = time, note_off = time + length, note_length = length)
head(silence_2) ## # A tibble: 6 x 5
## note track note_on note_off note_length
## <int> <int> <dbl> <dbl> <dbl>
## 1 79 2 0 384 384
## 2 79 2 384 768 384
## 3 79 2 1322 1343 21
## 4 79 2 6912 6960 48
## 5 79 2 7152 7296 144
## 6 79 2 11520 11904 384Etape 3
Pour l’étape 3, nous ne joignons pas la table de fréquence. Nous allons ici calculer la durée des silences. Avant nous enregistrons dans un vecteur la durée complète du morceau.
track_length <- max(midinotes$time) + last(midinotes$length)
track_length## [1] 36864Puis nous créons 2 nouvelles colonnes, silence_on et silence_off.
Nous remplaçons la valeur NA obtenue avec lead(note_on). La fonction lead()
décalle les valeurs d’une rangée. Ce qui permet par la suite de calculer
la longueur de chaque silence dans une nouvelle colonne silence_length.
silence_3 <- silence_2 %>%
mutate(silence_on = note_off, silence_off = lead(note_on)) %>%
mutate(silence_off = replace_na(silence_off, track_length)) %>%
mutate(silence_length = silence_off - silence_on)
tail(silence_3)## # A tibble: 6 x 8
## note track note_on note_off note_length silence_on silence_off silence_length
## <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 79 2 20544 20714 170 20714 21840 1126
## 2 79 2 21840 21888 48 21888 23040 1152
## 3 79 2 23040 23328 288 23328 24192 864
## 4 79 2 24192 24240 48 24240 26112 1872
## 5 79 2 26112 26304 192 26304 34464 8160
## 6 79 2 34464 34560 96 34560 36864 2304Etape 4
Nous sélectionnons toutes les colonnes silence avec select_at(vars(starts_with("silence"))).
Certaines observations ont silence_length == 0. Nous les filtrons.
Avec transmute() nous renommons les colonnes et ajoutons une colonne note avec la valeur NA.
Nous obtenons une table de notes “vides” ou silencieuses.
silence_4 <- silence_3 %>%
select_at(vars(starts_with("silence"))) %>%
filter(silence_length != 0) %>%
transmute(note_on = silence_on, note_length = silence_length, note = NA)
head(silence_4)## # A tibble: 6 x 3
## note_on note_length note
## <dbl> <dbl> <lgl>
## 1 768 554 NA
## 2 1343 5569 NA
## 3 6960 192 NA
## 4 7296 4224 NA
## 5 12480 96 NA
## 6 12842 1078 NAEtape 5
Dernière opération. Il y a une petite subtilité que j’ai mis longtemps à comprendre.
Si on récapitule, le but est d’avoir pour chaque note et silence l’ensemble des ondes.
Une fois l’ensemble des ondes synthétisées nous pouvons les combiner afin d’avoir
la séquence complète de chaque note. Mais voilà lorsque j’additionnais l’ensemble des séquences,
j’obtenais une erreur. Les séquences individuelles n’avaient pas la même longueur
donc la même durée. Pour simplifier, l’onde entière (c’est-à-dire note + silence d’une note,
par ex. la note 79) n’avait pas la même longueur que l’onde complète de la note 81.
En réalité pour pouvoir additionner, c’est-à-dire mettre une note sur l’autre,
nous devons avoir des ondes de même longueur, sinon cela ne marche pas.
Exemple d’addition de 2 ondes de durée différente et de fréquence différente :
synth(f = 8000, cf = 440, d = 1, a = 1, output = "Wave") +
synth(f = 8000, cf = 536, d = .5, a = 1, output = "Wave")Si vous exécutez le code ci-dessus, vous obtiendrez un message d’erreur : “Waves must be of equal length for Arithmetics”.
Exemple d’addition de 2 ondes de même durée et de fréquence différente :
synth(f = 8000, cf = 440, d = 1, a = 1, output = "Wave") +
synth(f = 8000, cf = 536, d = 1, a = 1, output = "Wave")##
## Wave Object
## Number of Samples: 8000
## Duration (seconds): 1
## Samplingrate (Hertz): 8000
## Channels (Mono/Stereo): Mono
## PCM (integer format): TRUE
## Bit (8/16/24/32/64): 16Ici ça marche.
En fait, le problème vient de la fonction d’ajout de silence addsilw() qui ajoute une observation.
Ce qui nous donne une table d’onde avec un échantillon en plus et modifie aussi la durée.
Démonstration :
addsilw(0, f = 100, d = 1, at = "end", output = "Wave")##
## Wave Object
## Number of Samples: 101
## Duration (seconds): 1.01
## Samplingrate (Hertz): 100
## Channels (Mono/Stereo): Mono
## PCM (integer format): TRUE
## Bit (8/16/24/32/64): 16Pour résoudre le problème, nous supprimons la première observation de la table générée, ou onde. Je vois que je vous ai perdu. Rappelez-vous, notre onde n’est qu’une table de valeur entre -1 et 1. Le résultat de la fonction sinus. Pour en avoir le coeur net, nous pouvons afficher la structure de l’objet “Wave” généré.
synth(f = 8000, cf = 440, d = 1, a = 1, output = "Wave")@left %>%
str()## num [1:8000] 0 0.339 0.637 0.861 0.982 ...Nous avons bien 8,000 valeurs. Revenons à cette dernière étape.
Nous mappons la fonction addsilw() sur chaque silence en indiquant
pour l’argument de la durée d = .x/384. N’oublions pas d’ajouter à la fin
de la fonction le sélecteur [-1, ] pour supprimer la première observation
et conserver exactement un silence de bonne longueur.
silence_5 <- silence_4 %>%
mutate(synth = map(note_length, ~ addsilw(0, f = 8000, d = (.x/384), at = "end", output = "Wave")[-1, ]))
head(silence_5)## # A tibble: 6 x 4
## note_on note_length note synth
## <dbl> <dbl> <lgl> <list>
## 1 768 554 NA <Wave>
## 2 1343 5569 NA <Wave>
## 3 6960 192 NA <Wave>
## 4 7296 4224 NA <Wave>
## 5 12480 96 NA <Wave>
## 6 12842 1078 NA <Wave>11. Note et silence
Etape 1
Nous avons maintenant nos 2 tables. Une table avec les ondes de la note jouée.
Une autre table avec les silences. Il nous reste plus qu’à joindre les 2 tables
ensemble. Nous prendrons l’étape 4 pour la note puisque l’étape 5 consistait à joindre l’ensemble des ondes en une seule onde. Nous utilisons la fonction bind_rows()
du package {dplyr}. Cela consiste à joindre les rangées des 2 tables
dans une seule table que nous nommons : note_and_silence.
note_and_silence_1 <- note_4 %>%
bind_rows(silence_5)Etape 2
Avec la fonction arrange(), nous organisons la table selon l’apparition
chronologique de la note et des silences. Observez la note NA qui
correspond à notre silence.
note_and_silence_2 <- note_and_silence_1 %>%
arrange(note_on)
head(note_and_silence_2)## # A tibble: 6 x 5
## note note_on note_length freq synth
## <dbl> <dbl> <dbl> <dbl> <list>
## 1 79 0 384 784. <Wave>
## 2 79 384 384 784. <Wave>
## 3 NA 768 554 NA <Wave>
## 4 79 1322 21 784. <Wave>
## 5 NA 1343 5569 NA <Wave>
## 6 79 6912 48 784. <Wave>Etape 3
la note 79 est une des notes jouées dès le début du morceau.
Pour preuve nous avons une onde synthétise pour note_on == 0.
Toutes les notes de la partition ne commencent pas au temps 0.
Ce qui veut dire que nous devons ajouter un silence supplémentaire.
Sachez que dans cet exemple avec la note 79, cela n’a pas
beaucoup d’intérêt puisque nous avons une note jouée en note_on == 0.
Mais pour les autres notes, cela est essentiel pour garantir une onde synthétisée
de même longueur pour les additionner ensemble par la suite.
3 étapes seront nécessaires. Premièrement, créer une table avec tibble(),
puis deuxièmement, générer un silence pour la période entre 0 et le moment
où la note est jouée pour la première fois. Enfin, nous joignons cette table
avec la table note_and_silence.
note_and_silence_3 <- note_and_silence_2 %>%
arrange(note_on) %>%
bind_rows(
tibble(note_on = 0 , note_length = first(note_and_silence_1$note_on), note = NA) %>%
mutate(synth = map(note_length, ~ addsilw(0, f = 8000, d = (note_length/384), output = "Wave", at = "end")[-1, ])
))
head(note_and_silence_3)## # A tibble: 6 x 5
## note note_on note_length freq synth
## <dbl> <dbl> <dbl> <dbl> <list>
## 1 79 0 384 784. <Wave>
## 2 79 384 384 784. <Wave>
## 3 NA 768 554 NA <Wave>
## 4 79 1322 21 784. <Wave>
## 5 NA 1343 5569 NA <Wave>
## 6 79 6912 48 784. <Wave>Etape 4
Dernière étape pour avoir notre objet Wave de la note 79.
Nous arrangeons dans l’ordre chronologique nos ondes avec arrange(note_on).
Nous sortons chaque objet Wave imbriqué dans la colonne synth avec
la fonction pull(). Puis comme pour l’étape 5 de la section note,
nous utilisons la fonction reduce() pour joindre chaque onde avec la
jointure précédente et ne garder au final qu’un seul objet.
note_and_silence_4 <- note_and_silence_3 %>%
arrange(note_on) %>%
pull(synth) %>%
reduce(bind)
note_and_silence_4 ##
## Wave Object
## Number of Samples: 767999
## Duration (seconds): 96
## Samplingrate (Hertz): 8000
## Channels (Mono/Stereo): Mono
## PCM (integer format): TRUE
## Bit (8/16/24/32/64): 16Etape 5
Nous allons pouvoir écouter ce que cela donne. Cela ne donne pas grand-chose.
De plus il y a beacoup de silence pour cette note 79.
12. La fonction extract_melody()
Nous n’allons certainement pas faire toutes ces manipulations pour chaque note.
Comme dirait Hadley, si une opération est répétée 3x, développez une fonction.
C’est exactement ce que nous allons faire ici. Nous avons passé en revue chaque étape.
Cette fonction n’aura donc aucun secret pour vous. Nous ajoutons pour cette fonction
les arguments am et fm issus de la fonction synth().
extract_melody <- function(df, x, y, sf, div, signal, shape, am, fm, harmonics) {
track_length <- max(df$time) + last(df$length)
# extract silence
silence <- df %>%
as_tibble() %>%
select(-channel, -notename, -velocity) %>%
filter(note == x) %>%
filter(track == y) %>%
transmute(note, track, note_on = time, note_off = time + length, note_length = length) %>%
mutate(silence_on = note_off, silence_off = lead(note_on)) %>%
mutate(silence_off = replace_na(silence_off, track_length)) %>%
mutate(silence_length = silence_off - silence_on) %>%
select_at(vars(starts_with("silence"))) %>%
filter(silence_length != 0) %>%
transmute(note_on = silence_on, note_length = silence_length, note = NA) %>%
mutate(synth = map(note_length, ~ addsilw(0, f = sf, d = (./div), at = "end", output = "Wave")[-1, ]))
# extract note
note <- df %>%
as_tibble() %>%
select(-channel, -notename, -velocity) %>%
filter(note == x) %>%
filter(track == y) %>%
transmute(note, track, note_on = time, note_off = time + length, note_length = length) %>%
left_join(note_table_cleaned, by = "note") %>%
select(note, note_on, note_length, freq) %>%
mutate(synth = map2(freq, note_length, ~ synth(f = sf, d = (.y/div), cf = .x, signal = signal, shape = shape, am = am, fm = fm, harmonics = harmonics, output = "Wave")))
# merge note + silence
note_and_silence <- note %>%
bind_rows(silence) %>%
arrange(note_on) %>%
bind_rows(
tibble(note_on = 0 , note_length = first(note$note_on), note = NA) %>%
mutate(synth = map(note_length, ~ addsilw(0, f = sf, d = (note_length/div), output = "Wave", at = "end")[-1, ])
)) %>%
arrange(note_on) %>%
select(synth) %>%
unlist() %>%
reduce(bind)
return(note_and_silence)
}13. Synthétiser l’ensemble de la partition.
Récapitulons. Nous avons maintenant à notre disposition la fonction extract_melody()
qui nous permet d’extraire une onde équivalente à la durée de la partition pour chaque note.
Ce qui nous reste à faire c’est de le faire pour chaque note présente dans la partition.
Plus simplement dit, extraire la mélodie de la note 79, 81, 69 etc.
Etape 1
Nous récupérons notre jeu de donnée midinotes pour en extraire la valeur des
notes présentes dans la partition avec la fonction distinct().
full_melody_1 <- midinotes %>%
distinct(note, track)
head(full_melody_1)## note track
## 1 79 2
## 2 81 2
## 3 83 2
## 4 78 2
## 5 76 2
## 6 74 2Etape 2
Cette étape consiste à exécuter notre fonction extract_melody() sur l’ensemble
des notes de la partition via map2()sur la table full_melody_1 générée en étape 1
et d’enregistrer le résultat dans la colonne melody.
full_melody_2 <- full_melody_1 %>%
mutate(melody = map2(note, track, ~ extract_melody(df = midinotes,
x = .x, y = .y,
sf = 4000,
div = 386,
signal = "sine",
shape = "sine",
am = c(0, 0, 0),
fm = c(0, 0, 0, 0, 0),
harmonics = c(1))))
head(full_melody_2)## note track melody
## 1 79 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>
## 2 81 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>
## 3 83 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>
## 4 78 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>
## 5 76 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>
## 6 74 2 <S4 class 'Wave' [package "tuneR"] with 6 slots>Etape 3
En travaillant sur ce projet, j’ai été confronté à une deuxième problématique.
Après le problème de longueur d’onde générée par la fonction addsillw(),
nous sommes face à un autre problème de longueur. Pour vous montrer cela,
extrayons la longueur de l’onde pour chaque note de la partition.
full_melody_3 <- full_melody_2 %>%
mutate(synth_length = map(melody, length)) %>%
unnest(synth_length)
head(full_melody_3)## # A tibble: 6 x 4
## note track melody synth_length
## <int> <int> <list> <int>
## 1 79 2 <Wave> 382001
## 2 81 2 <Wave> 382003
## 3 83 2 <Wave> 382009
## 4 78 2 <Wave> 382003
## 5 76 2 <Wave> 381998
## 6 74 2 <Wave> 382000Que voyez-vous ? Simplement les longueurs des objets Wave ils diffèrent.
Je ne sais pas exactement pourquoi, mais c’est sans doute à cause de l’opération
qui consiste à transformer la durée des notes en seconde avant de générer l’objet Wave.
Le résultat de cette opération est probablement arrondi et donc nous donne des variations
de longueur. Que faire ? Bien, l’idée est de “couper” comme à l’époque du cinéma en bobine
la longueur de chaque objet Wave à la longueur de l’objet le moins long avec une fonction
écrite sous forme de formula : ~ .x[1:min(synth_length), ].
Cette fonction coupe chaque objet à la longueur de notre plus petit objet.
En réalité cela consiste à prendre une partie de l’objet par le sélecteur :
[1:min(synth_length), ].
full_melody_4 <- full_melody_3 %>%
transmute(track, melody = map(melody, ~ .x[1:min(synth_length), ]))
head(full_melody_4)## # A tibble: 6 x 2
## track melody
## <int> <list>
## 1 2 <Wave>
## 2 2 <Wave>
## 3 2 <Wave>
## 4 2 <Wave>
## 5 2 <Wave>
## 6 2 <Wave>Etape 4
Nous allons maintenant extraire pour chaque track ou “main”, l’ensemble des objets Wave.
Puis, composer la mélodie complète pour chaque main en additionnant les objets et non en les organisant comme les wagons d’un train, l’un derrière l’autre. Il s’agit bien de superposer les objets l’un sur l’autre pour générer un seul objet. Nous utiliserons donc la fonction sum()
et pas bind() comme ce fût pour les étapes “note” et “silence”.
Chaque main sera enregistrée dans les objets left_channel et right_channel.
left_channel <- full_melody_4 %>%
filter(track == 2) %>%
pull(melody) %>%
reduce(`+`)
right_channel <- full_melody_4%>%
filter(track == 3) %>%
pull(melody) %>%
reduce(`+`)Etape 5
Grâce à la fonction stereo(), nous couplons les 2 objets en un seul et le normalisons.
Pour avoir une mélodie plus distincte pour chaque main, nous jouons avec
la fonction panorma(), une autre fonction du package {tuneR}.
aria_melody <- stereo(right_channel, left_channel) %>%
normalize(unit = "16") %>%
panorama(-.6)Ecoutons ce que cela donne.
J’adore.
14. Fonction finale
Nous voici à la fin de cette 2e partie. Pour bien terminer notre travail,
nous allons synthétiser toutes les étapes en 1 seule fonction play_midi_notes().
Nous utiliserons cette fonction pour la 3e partie de ce long article, l’application Shiny.
play_midi_notes <- function(midi_notes, left, right, sf, div, signal, shape, am, fm, harmonics, pan) {
tracks_wav <- midi_notes %>%
distinct(note, track) %>%
mutate(melody = map2(note, track, ~ extract_melody(df = midi_notes,
x = .x, y = .y,
sf = sf,
div = div,
signal = signal,
shape = shape,
am = am,
fm = fm,
harmonics = harmonics))) %>%
mutate(synth_length = map(melody, length)) %>%
unnest(synth_length) %>%
transmute(track, melody = map(melody, ~ .x[1:min(synth_length), ]))
left_channel <- tracks_wav %>%
filter(track == left) %>%
select(melody) %>%
unlist() %>%
reduce(`+`)
right_channel <- tracks_wav %>%
filter(track == right) %>%
select(melody) %>%
unlist() %>%
reduce(`+`)
stereo(right_channel, left_channel) %>% normalize(unit = "16") %>% panorama(pan = pan)
}Si vous avez aimé, si vous avez des commentaires, n’hésitez pas.